45 баллов! Помогите пожалуйста решить задачи с подробным объяснением

Ответы
Ответ:
1. 2√6
2.AC=AB=8√3
3. 120 см²
Объяснение:
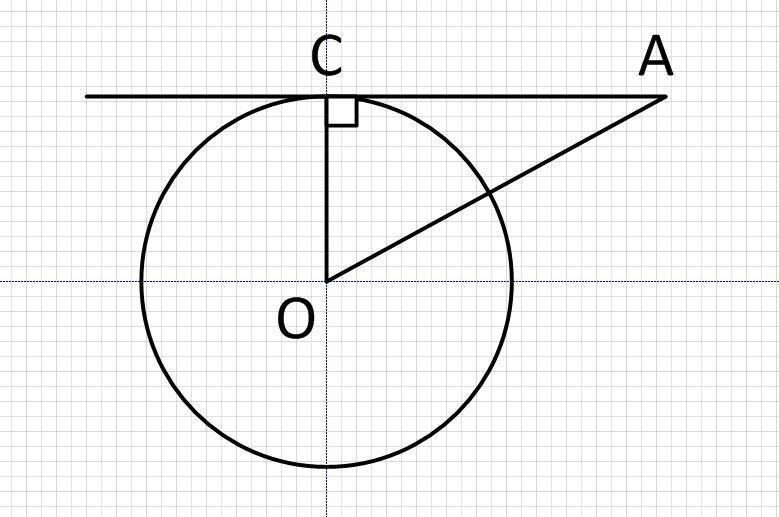
1. В треугольнике ACO CO является радиусом, проведенным из центра окружности в точку касания, он перпендикулярен касательной. Таким образом указанный треугольник прямоугольный, и найти радиус CO можно используя теорему Пифагора:
OA²=AC²+CO²
CO²=OA²-AC²
CO=√(OA²-AC²)
CO=√(6²-(2√3)²)
CO=√(36-4*3)
CO=√24=2√6
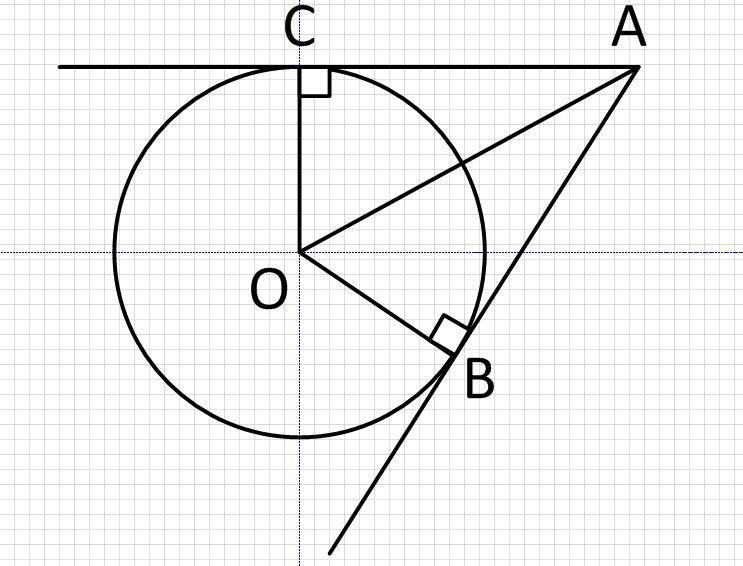
2. Рассмотрим треугольники ACO и ABO в них ОС и ОВ - радиусы опушенные из центра окружности в точку касания, будут перпендикулярны соответствующим касательным AC и AB.
Прямоугольные треугольники ACO и ABO равны по катету CO=CB (как радиусы) и гипотенузе OA.
∠CAO=∠BAO=∠CAB/2=60/2=30°
Катеты лежащие напротив угла в 30° равны половине гипотенузы, стало быть, AO=2*СО= 2*8= 16 см.
По теореме Пифагора
AO²= CO²+AC²
AC²=AO²-CO²
AC=√(AO²-CO²)
AC=√(16²-8²)
AC=√192
AC=8√3 см
Так как выше обозначенные треугольники равны AC=AB=8√3 см
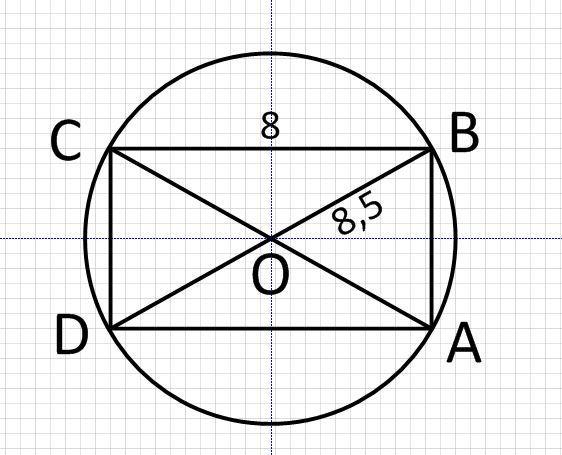
3. Точка пересечения диагоналей прямоугольника, является центром описанной окружности. Диагонали прямоугольника пересекаясь делятся пополам. Из чего следует, что BO=DO=r, DB=2*r=17см.
По теореме Пифагора
DB²=CB²+CD²
CD=√(DB²-CB²)
CD=√(17²-8²)=√225=15 см
Площадь прямоугольника равна
S=CD*CB=15*8=120 см²
4. Не понятно что за угол Р?
2.AC=AB=8√3
3. 120 см²