Question

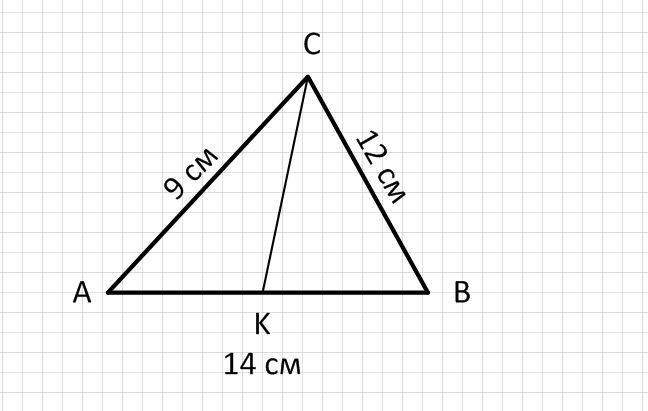
CK - биссектриса треугольника ABC, AB = 14 см, AC = 9 см, BC = 12 см. Найдите AK и KB

Помогите пожалуйста

Answer 1

Как известно, биссектриса CK делит сторону AB на отрезки m=AK и m=KB, пропорциональные сторонам AC и BC:

m:n=AC:BC.

Кроме того, m+n=AB. Из этих двух условий находим m и n:

$m=\frac{AB\cdot AC}{AC+BC};\ n=\frac{AB\cdot BC}{AC+BC}.$

В нашем случае $AK=m=\frac{14\cdot 9}{9+12}=6;\ KB=AB-AK=14-6=8.$

Ответ: AK=6; KB=8

Answer 2

Ответ:

AK=6 см

KB=8 см

Объяснение:

Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам.

В нашем случае противоположная сторона это AB, а прилегающие стороны это AC и BC получаем:

AK/KB = AC/BC,

AK*BC=KB*AC, так как KB=14-AK,

AK*BC=(14-AK)*AC

подставим имеющиеся данные:

AK*12=(14-AK)*9

AK*12=14*9-AK*9

AK*12+AK*9=126

AK(12+9)=126

AK=126/21

AK=6 см

Осталось найти KB:

KB=14-AK=14-6=8 см