Предмет: Геометрия,
автор: kapdkin2005
Доведите тождество: (cos^3B-sin^3B)/(1+sinBcosB)=cosB-sinB
Приложения:
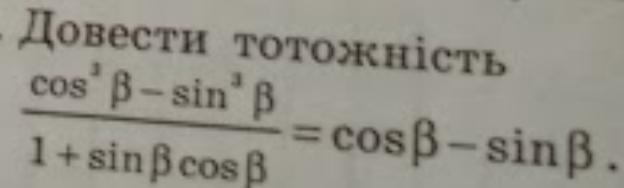
Ответы
Автор ответа:
9
Распишем левую часть и докажем, что она равна правой.
(cos³β-sin³β)/(1+sinβcosβ)=
(cosβ-sinβ)(cos²β+cosβ*sinβ+sin²β)/(1+sinβcosβ)=
(cosβ-sinβ)(1+cosβsinβ)/(1+cosβsinβ)=(cosβ-sinβ) , что и требовалось доказать.
При доказательстве пользовался разложением разности кубов и основным тригонометрическим тождеством, Синус в квадрате бэтта плюс Косинус в квадрате бэтта равно 1
Похожие вопросы
Предмет: Химия,
автор: ilaelizarov362
Предмет: Английский язык,
автор: helper228567
Предмет: Математика,
автор: demetradch
Предмет: Литература,
автор: реал12
Предмет: Математика,
автор: Сашкенсия