Предмет: Геометрия, автор: Аноним

Здравствуйте! Срочно! Полное решение не обязательно, можно по короче или ответ. Ерунду не писать! Спасибо) Дам 30 баллов.

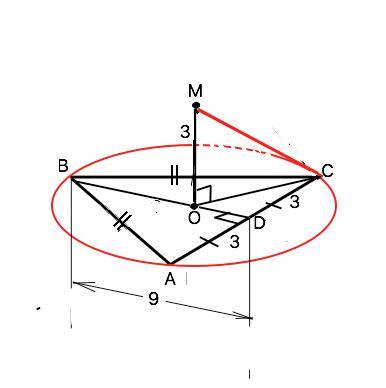
В равнобедренном треугольнике ABC основание AC=6, а высота BD=9. Точка M равноудалена от всех вершин данного треугольника и находится на расстоянии
3 от плоскости, в которой он лежит. Вычислите расстояние l от точки M до вершины C треугольника. В ответ запишите значение l2

Hrisula: По правилам сообщества Знания ответ не может считаться верным только по конечному результату и подлежит удалению. Решение должно содержать расчеты и необходимые пояснения. Полный ответ поможет сотням других участников.

Hrisula: Что означает "В ответ запишите значение l2"? Может, l² ( т.к. в ответе получается число под корнем)

Ответы

Автор ответа: Hrisula

Ответ: l²=34

Объяснение: Точка M равноудалена от всех вершин данного треугольника, следовательно, все наклонные из М к вершинам, а, значит, и к плоскости треугольника, равны, поэтому равны и их проекции ОС=ОВ=ОА и равны радиусу описанной около ∆ АВС окружности.

Искомое расстояние МС - гипотенуза прямоугольного ⊿ МОС. Для её нахождения нужно найти катет ОС этого треугольника. ОС=R.

Формула радиуса описанной окружности R=a•b•c/4S ( где а, b и с - стороны треугольника).

S=BD•AC:2=9•6:2=27

Боковые стороны ∆ (АВС) найдём из ⊿ АВD. Высота ВD в равнобедренном треугольнике ещё и медиана (свойство)

По т.Пифагора. АВ=√(BD²+AD²)=√(9²+3²)=√90

R=(√90•√90•6):4•27= 5

ОС=5 ⇒ МС²=(MO²+OC²)=3²+5²=34 ⇒ l²=34

Приложения: