Предмет: Алгебра,
автор: catumida2011
Вычислите предел функции
Приложения:
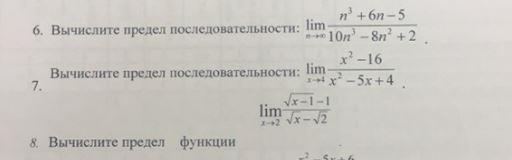
спасибо
Ответы
Автор ответа:
0
Ответ:
Объяснение:
6. вычислите предел последовательности
6. вычислите предел последовательности
7. Вычислите предел функции
Похожие вопросы
Предмет: Русский язык,
автор: myrzabekovazanat2
Предмет: Биология,
автор: Kolia0Flayer
Предмет: Биология,
автор: 123margarita123
Предмет: Химия,
автор: anna12319
Предмет: Информатика,
автор: оксик46
7. раскладываете х-4 сокращается
8. непределенность 0/0 используйте Лопиталя