нужна помощь ;)!!!!!!
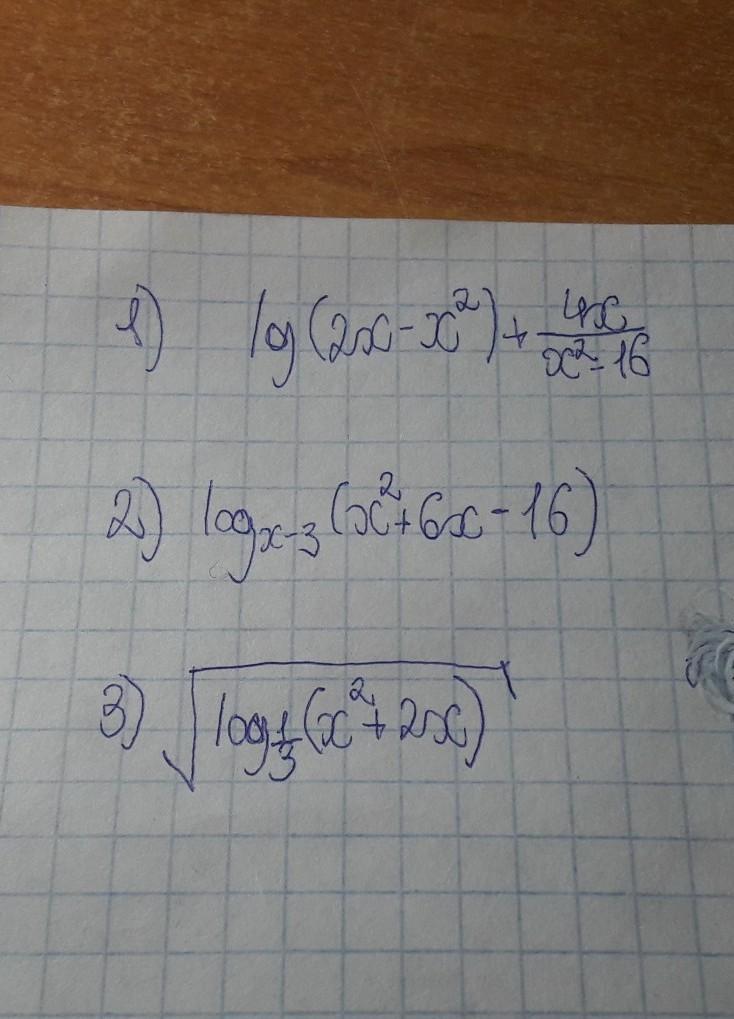
Ответы
1) 2х-х²>0
х²-16≠0
Эти условия должны выполняться одновременно.
х*(2-х)>0, первое неравенство решим методом интервалов, положительное подлогарифмическое выражение достигается, когда х∈((0;2)), а второе, когда х≠±4, иначе не будет существовать дробь, но в пересечении ОДЗ такая х∈(0;2)
2) х-3≠1
х-3>0
х²+6х-16>0
после преобразования первое условие х≠4
второе х>3
третье тоже решается с помощью метода интервалов,
Найдем корни левой части неравенства
х₁,₂=-3±√(9+16)=-3±5 Корни -8 и 2 разобьют область определения на интервалы (-∞;-8);(-8;2);(2;+∞) установим знаки на каждом из них.
Положительный трехчлен при х∈(-∞;-8)∪(2;+∞)
Найдем теперь пересечение всех трех условий. т.е. одновременное их выполнение. ОДЗ получим (3;4)∪(4;+∞)
3) подкоренное выражение неотрицательно, когда ㏒₁/₃(х²+2х)≥0, второе условие (х²+2х)>0
Чтобы решить неравенство первое, вспомним, что логарифм. функция при основании одна треть будет убывающей, поэтому
х²+2х≤(1/3)°, х²+2х-1≤0
Приравняем к нулю левую часть. х²+2х-1=0
х₁,₂=-1±√(1+1)
Корни -1-√2 и -1+√2 разобьют обл. опр. на интервалы
(-∞;-1-√2);(-1-√2;-1+√2);(-1+√2;+∞)
Решением неравенства х²+2х-1≤0 будет отрезок [-1-√2;-1+√2], а решением неравенства (х²+2х)>0, или х*(х+2)>0 будет объединение интервалов (-∞;-2)∪(2;+∞)
ОДЗ - это пересечение двух решений. Ею будет
[-1-√2;-2)∪(0;-1+√2]