Предмет: Математика,
автор: Аноним
Решите неравенство:
Приложения:
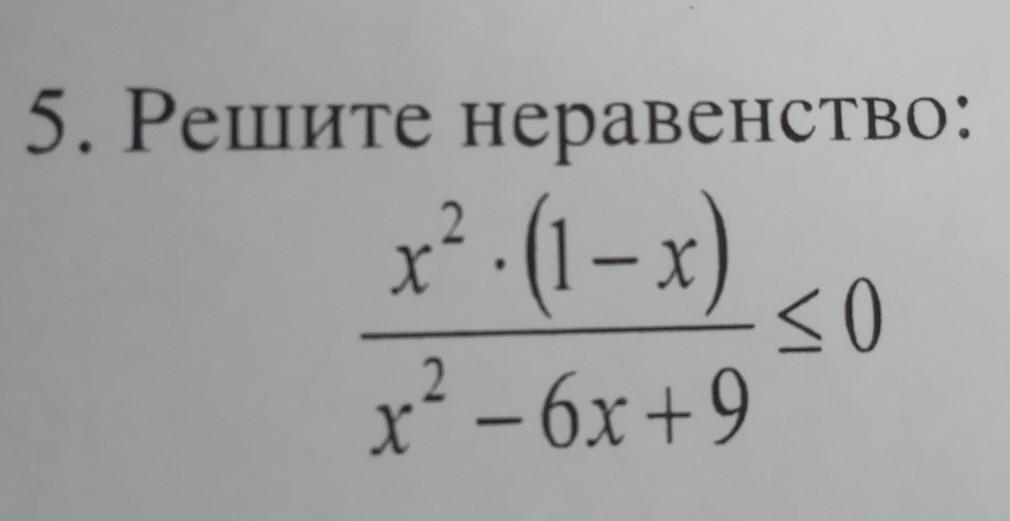
Ответы
Автор ответа:
1
Ответ: x=0, x∈[1;3)∪(3;+∞).
Пошаговое объяснение:
Числитель дроби обращается в 0 при x=0 и при x=1, знаменатель - при x²-6*x+9=(x-3)²=0, т.е. при x=3. Поэтому значения x=0 и x=1 удовлетворяют неравенству. Если x<0, то x²*(1-x)>0, и (x-3)²>0, поэтому на интервале (-∞;0) дробь положительна. Если 0<x<1, то x²*(1-x)>0 и (x-3)²>0, поэтому на интервале (0;1) дробь также положительна. Если 1<x<3, то x²*(1-x)<0, а (x-3)²>0, так что на интервале (1;3) дробь отрицательна. Наконец, если x>3, то x²*(1-x)<0, а (x-3)²>0, так что на интервале (3;+∞) дробь также отрицательна. Значит, решением неравенства являются значение x=0 и интервалы x∈[1;3)∪(3;+∞).
Похожие вопросы
Предмет: Информатика,
автор: mar3071166068
Предмет: Обществознание,
автор: artyom1666
Предмет: Алгебра,
автор: colvin10
Предмет: Алгебра,
автор: сомон1
Предмет: Алгебра,
автор: Olim261323