Question

ПОМОГИТЕ ОЧЕНЬ НУЖНО!
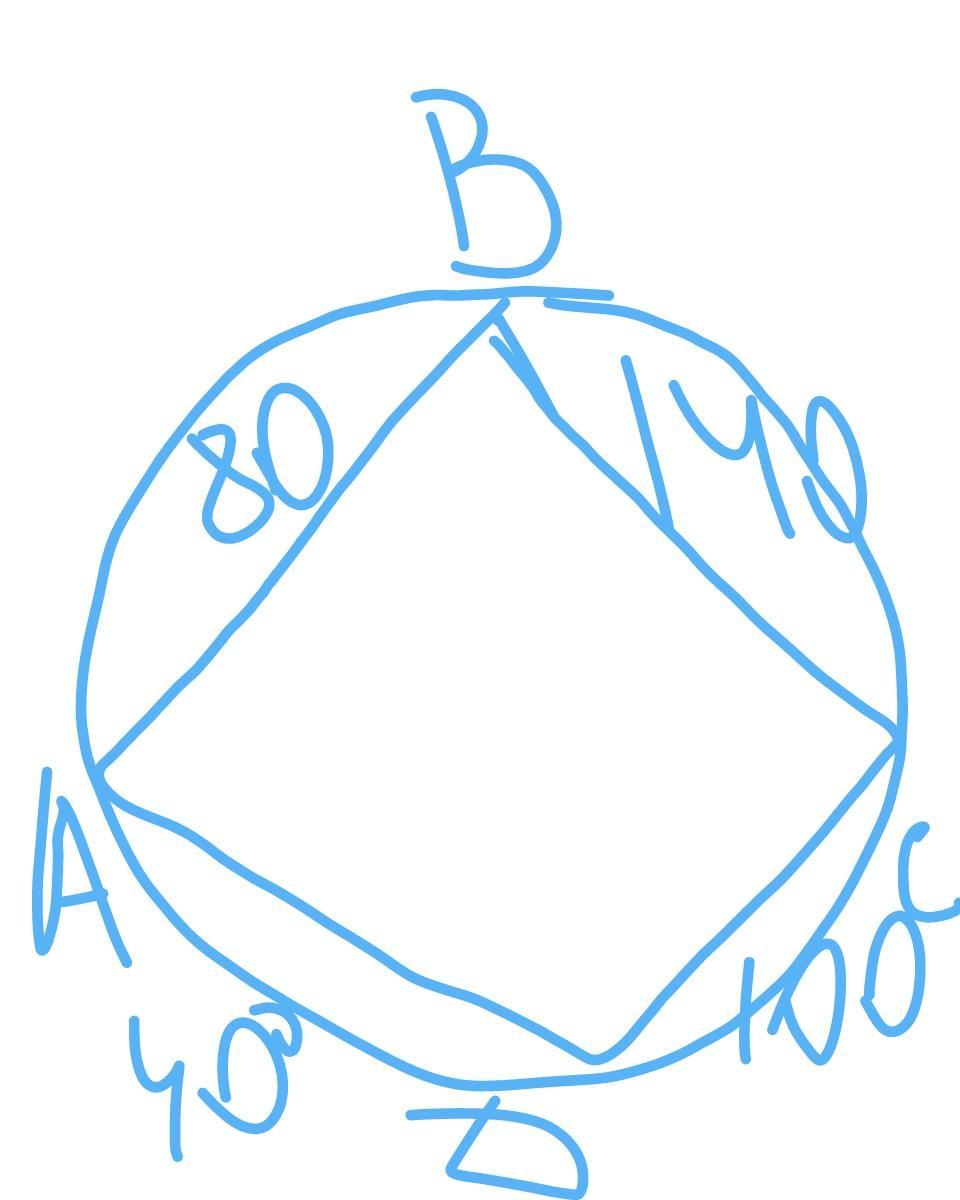
Стороны АВ, ВС, СD, вписанного четыре угольника ABCD отсекают дуги, градусные меры которых относятся как 4: 7: 5. Найдите углы четырехугольника, если сторона AD отсекает дугу в 40 градусов

Answer 1

Ответ:

60°,70°,110°,120°

Объяснение:

4k+7k+5k+40=360

16k=320

k=20

AB=20×4=80°

BC=20×7+140°

CD=20×5=100°

Всего окружность равна 360°

Поэтому сумма всех её дуг тоже равна 360°

Я взяла коэффициент пропорциональности и нашла все дуги.

Углы четырехугольника являются вписанными и равны половине дуги, на которую опираются.

∠В= 140÷2=70°

∠А=240÷2=120°

∠С=120÷2=60°

∠D=220÷2=110°