Question

Около равнобедренного треугольника, боковая сторона которого равна 16 корень из 5 см, описана окружность радиуса 20 см. Найдите площадь треугольника.
СРОЧНО! ЗАРАНЕЕ СПАСИБО!!!!

Answer 1

Ответ:

Sabc = 512 cм

Объяснение:

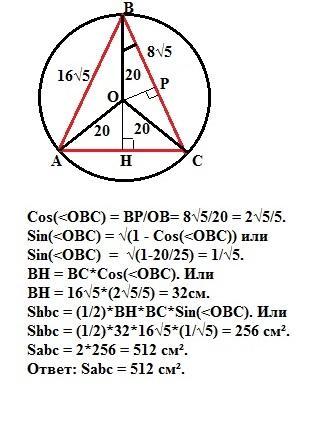
Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его сторонам. Тогда в прямоугольном треугольнике ОВР косинус угла ОВР равен отношению прилежащего катета ВР = 16√5/2 см к гипотенузе ОВ = 20см.

То есть Cos(<OBC) = 8√5/20 = 2√5/5.

В прямоугольном треугольнике ВНС катет ВН = ВС*Cos(<OBC) = 16√5*(2√5/5) = 32cм.

Площадь этого треугольника равна Shbc = (1/2)*BH*BC*Sin(<OBC).

Sin(<OBC) = √(1 - Cos(<OBC))  =  √(1-20/25) = 1/√5.  Тогда

Shbc = (1/2)*32*16√5*(1/√5) = 256 см². Это половина площади треугольника АВС (так как ВН - высота и медиана). Значит

Sabc = 2*256 = 512 см².