Предмет: Алгебра,
автор: Аноним
Найдите корни уравнения:
Приложения:
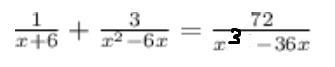
Ответы
Автор ответа:
1
1) Найдем область допустимых значений переменной:
x + 6 ≠ 0; x ≠ -6
x²- 6x = x(x - 6) ≠ 0; x ≠ 0; x ≠ 6;
x³ - 36x = x(x - 6)(x + 6) ≠ 0; x ≠ 0; x ≠ 6; x ≠ -6.
область допустимых значений переменной: x ≠ 0; x ≠ 6; x ≠ -6.
2) Приведем дроби уравнения к общему знаменателю x(x - 6)(x + 6):
(x(x-6) + 3(x+6) ) / x(x - 6)(x + 6) = 72 / x(x - 6)(x + 6);
x(x-6) + 3(x+6) = 72;
x² - 6x +3x +18 = 72;
x² - 3x - 54 =0; D = 3²+4*54 = 9 + 216 = 225 = 15²
x₁ = (3+15) / 2 = 18/2 = 9;
x₂ = (3-15) / 2 = -12/2 = -6 не является решением уравнения, так как не входит в область допустимых значений переменной уравнения.
Ответ: x = 9.
Похожие вопросы
Предмет: Математика,
автор: ag3237715
Предмет: История,
автор: mikolamarchuk707
Предмет: Українська мова,
автор: nikolyastremskaya
Предмет: Математика,
автор: кисябу
Предмет: Химия,
автор: 180820021