Question

вершина параболы ax2+bx+c имеет координаты x=4,y=-1 одна из ветвей параболы проходит через точку с координатами(0 и 15)найти уравнение пароболы
помоги пожалуйста

Answer 1

Уравнение параболы y=ax^2+bx+c
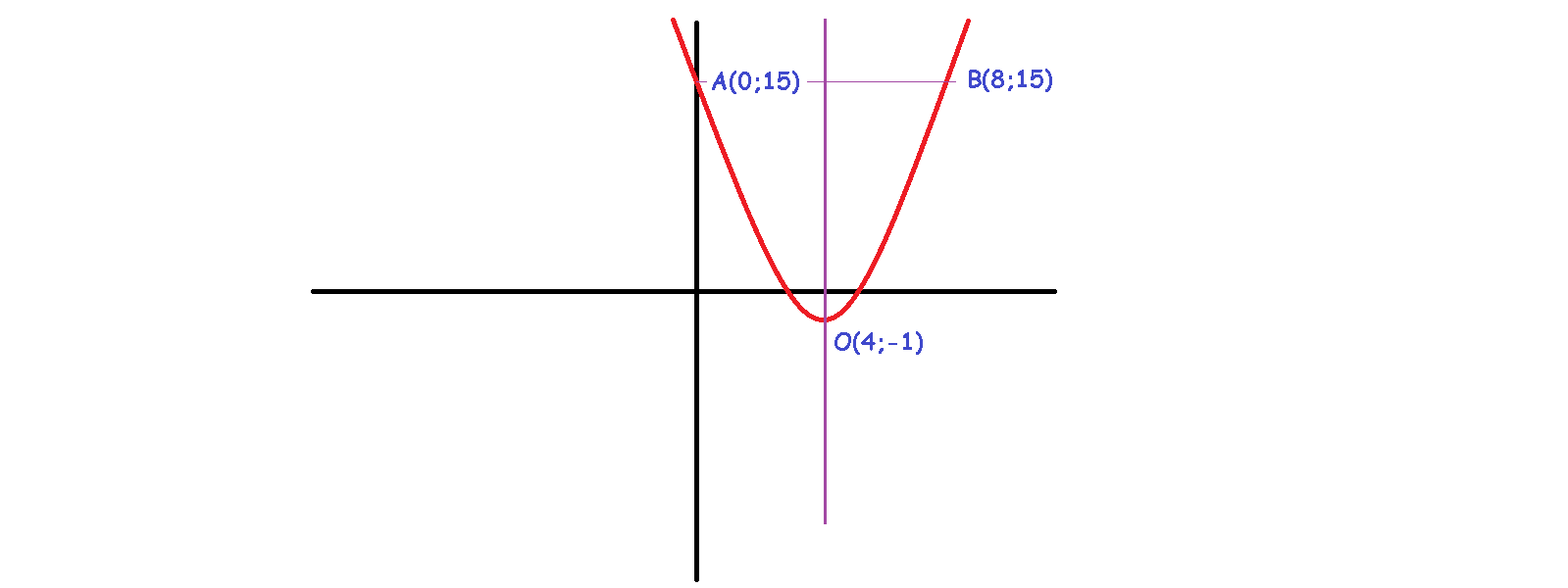
Известны две точки, через которые проходит парабола - O(4;-1) и А(0;15). Также известно то, что ветви параболы симметричны относительно прямой, проходящей через вершину перпендикулярно оси ох (см. рисунок). Значит третья точка, через которую проходит парабола - B(8;15)

Подставляем координаты этих трёх точек в уравнение параболы и получаем систему трёх уравнений с тремя неизвестными a,b,c.
$left{ begin{aligned} 4^2a+4b+c=-1\ 0^2a+0b+c=15\ 8^2a+8b+c=15\ end{aligned} right.\ left{ begin{aligned} 16a+4b+15=-1\ c=15\ 64a+8b+15=15\ end{aligned} right.\ left{ begin{aligned} 16a+4b=-16\ c=15\ 64a+8b=0\ end{aligned} right.\ left{ begin{aligned} 4a+b=-4\ c=15\ 8a+b=0\ end{aligned} right.\ left{ begin{aligned} 4a=4\ c=15\ b=-8a\ end{aligned} right.\ left{ begin{aligned} a=1\ c=15\ b=-8\ end{aligned} right.$
Уравнение параболы:
$y=x^2-8x+15$