Предмет: Математика,
автор: Аноним
Помогите решить дифференциальное уравнение 3981
Приложения:
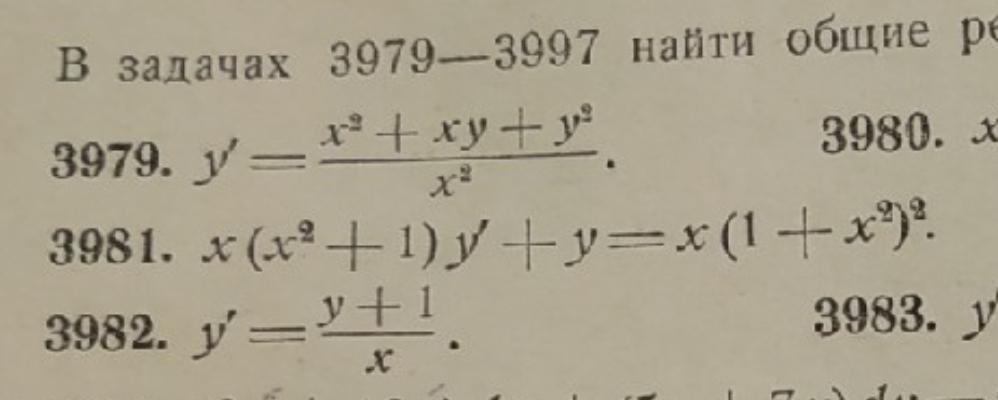
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Домножим комплектующий множитель.
Имеем
Похожие вопросы
Предмет: Математика,
автор: llearb7212
Предмет: Математика,
автор: pavluhha4440
Предмет: Обществознание,
автор: abduganievasafina
Предмет: География,
автор: PatriotPlay
Предмет: Литература,
автор: олик24