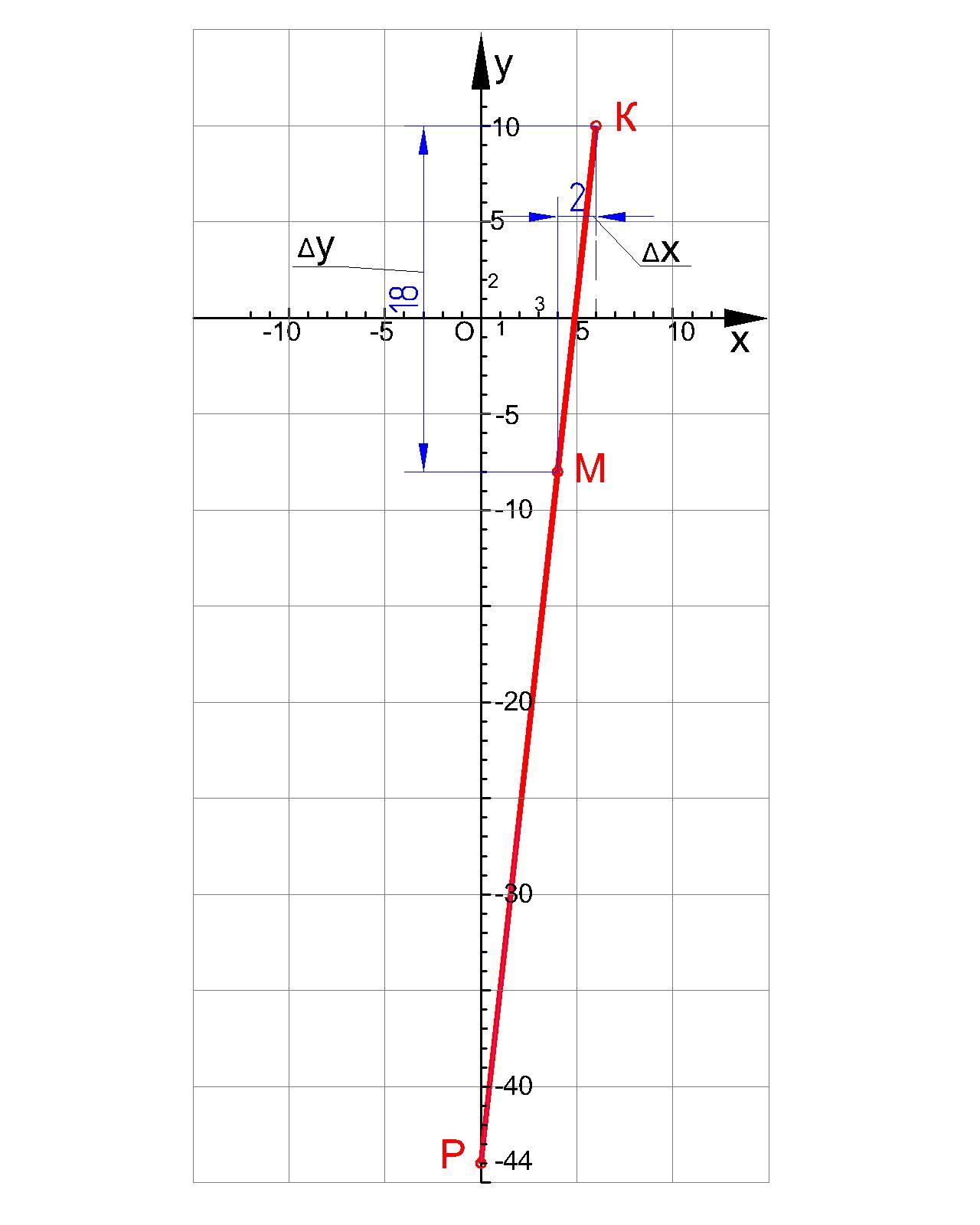
Точка М делит отрезок РК в отношении 2:1, начиная от точки Р . Найдите координаты точки Р , если точки М и К имеют соответственно координаты М (4;-8) P (6;10)
Ответы
Точка М делит отрезок РК в отношении 2 : 1, начиная от точки Р. Найдите координаты точки Р, если точки М и К имеют соответственно координаты М (4 ; - 8), K (6 ; 10).
============================================================
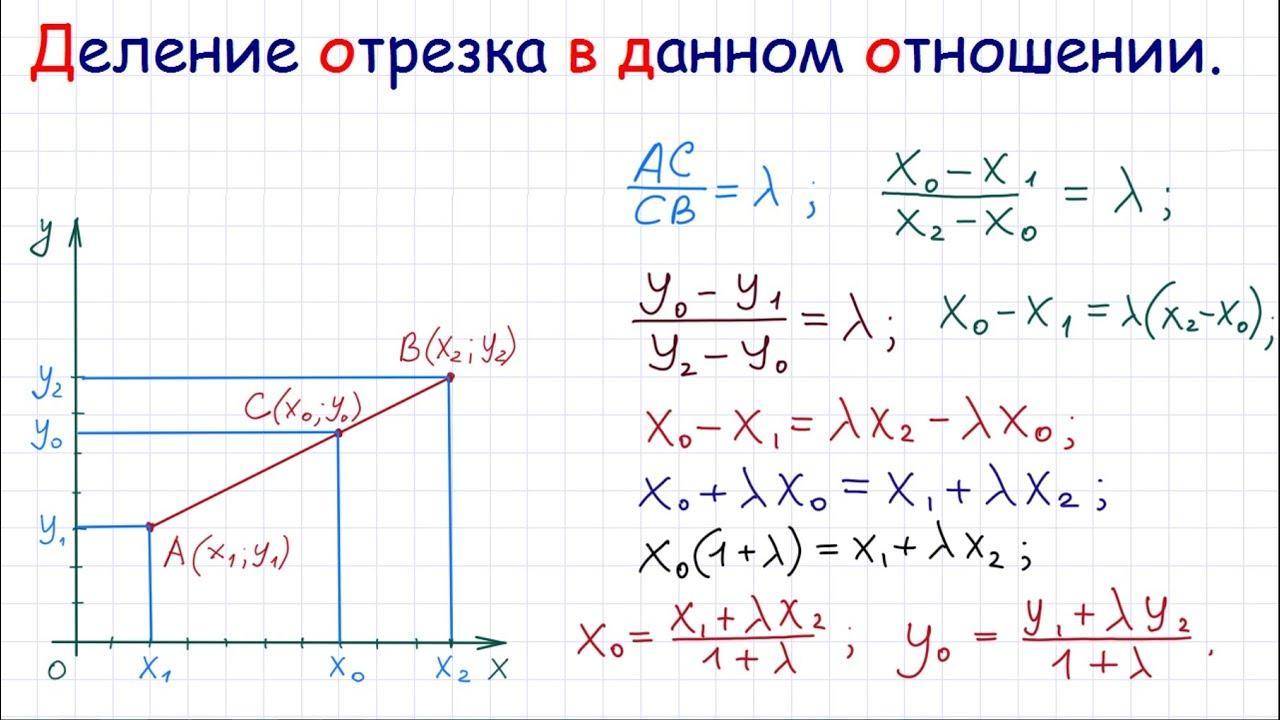
Если точка М делит отрезок РК в отношении РМ/МК = 2/1 = Y , то для нахождения координат точки М справедливы формулы:
Выражаем отсюда координаты точки Р:
Подставляем известные данные:
Координаты точки Р (0 ; - 44)
Ответ:
Р(0; -44)
Объяснение:
1) Представим координаты точки K как (х₁; у₁), точки М как (х₂; у₂), точки P как (х₃; у₃)
Найдём разницу соответствующих координат точек М и К:
Δх = (х₂ - х₁) = 4-6 = -2
Δу = (у₂ - у₁) = -8 - 10 = -18
Эти величины показывают нам как изменяется координата точки на отрезке, в зависимости от удаления т.М от т. K.
Так как известно, что т. М делит отрезок РК в отношении 2:1, начиная от т. Р, то коэффициент соотношения длин .
Тогда и изменение (дельта) координат от т.М до т.Р будет больше в 2 раза. Значит для вычисления координат т. Р можно записать выражения: