Question

Внутри равнобедренного треугольника ABC (AB=AC) взята точка P, такая что ∠ABP=∠PAC. Прямая AP пересекает BC в точке Q. Оказалось, что ∠BPQ в два раза больше ∠QPC. Докажите, что BQ=2·QC.

Answer 1

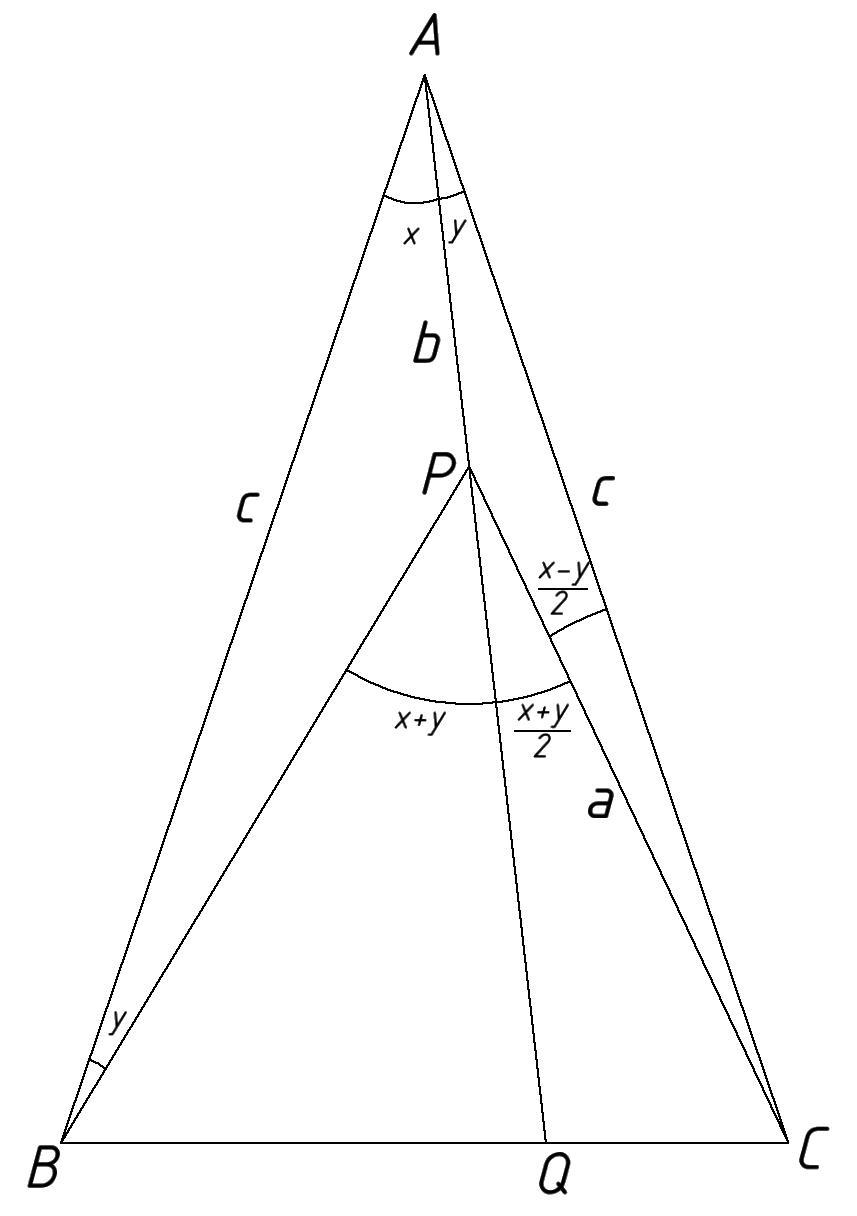
Все обозначения смотри на рисунке.

Из рассуждений  суммы  углов треугольника и смежных углов получаем что:

∠BPQ=x+y

∠QPC=(x+y)/2

По тем же рассуждениям можно получить,что:

∠PCA=(x-y)/2

Так же  сразу отметим что:

∠CPA=180-(x+y)/2 → sin∠CPA=sin(180-(x+y)/2)=sin ( (x+y)/2 )

∠BPA=180-(x+y) → sin∠BPA=sin(x+y)

Это  пригодится нам в дальнейшем.

Очевидно, что площади треугольников:

SΔBAQ/SΔQAC=BQ/QC ,тк  они имеют общую высоту.

Тогда:

1/2 *c*b*sin(x)/ (1/2 *c*b*sin(y) )=BQ/QC

sin(x)/sin(y)=BQ/QC

Запишем теоремы синусов  для ΔBAP  и ΔPAC:

1)c/sin(x+y)=b/sin(y)

2)c/sin( (x+y)/2)=a/sin(y)

3) a/sin(y)=b/sin(x-y)/2  → a/b=sin(y)/sin ((x-y)/2)

Поделим 2)  на 1)

sin(x+y)/sin ( (x+y)/2)=a/b

Откуда:

sin(x+y)/sin ( (x+y)/2)=sin(y)/sin ((x-y)/2)

2*sin( (x+y)/2 )*cos( (x+y)/2) /sin( (x+y)/2)=sin(y)/sin ((x-y)/2)

2*cos( (x+y)/2)=sin(y)/sin( (x-y)/2)

2*cos( (x+y)/2) * sin( (x-y)/2)=sin(y)

Применяем формулу произведения синуса на косинус:

2*1/2 *( sin( (x+y)/2 + (x-y)/2 ) +sin(  (x-y)/2 -(x+y)/2 ) )=sin(y)

sin(x)-sin(y)=sin(y)

sin(x)=2*sin(y)

sin(x)/sin(y)=2

BQ/QC=sin(x)/sin(y)=2

Таким  образом:

BQ=2*QC

ЧТД.