Предмет: Алгебра,
автор: kotodz333
Помогите решить примеры по математике.
Тема: Решение тригонометрических уравнений или тригонометрические уравнения
Очень срочно!
Могу точнее объяснить вопрос.
Приложения:
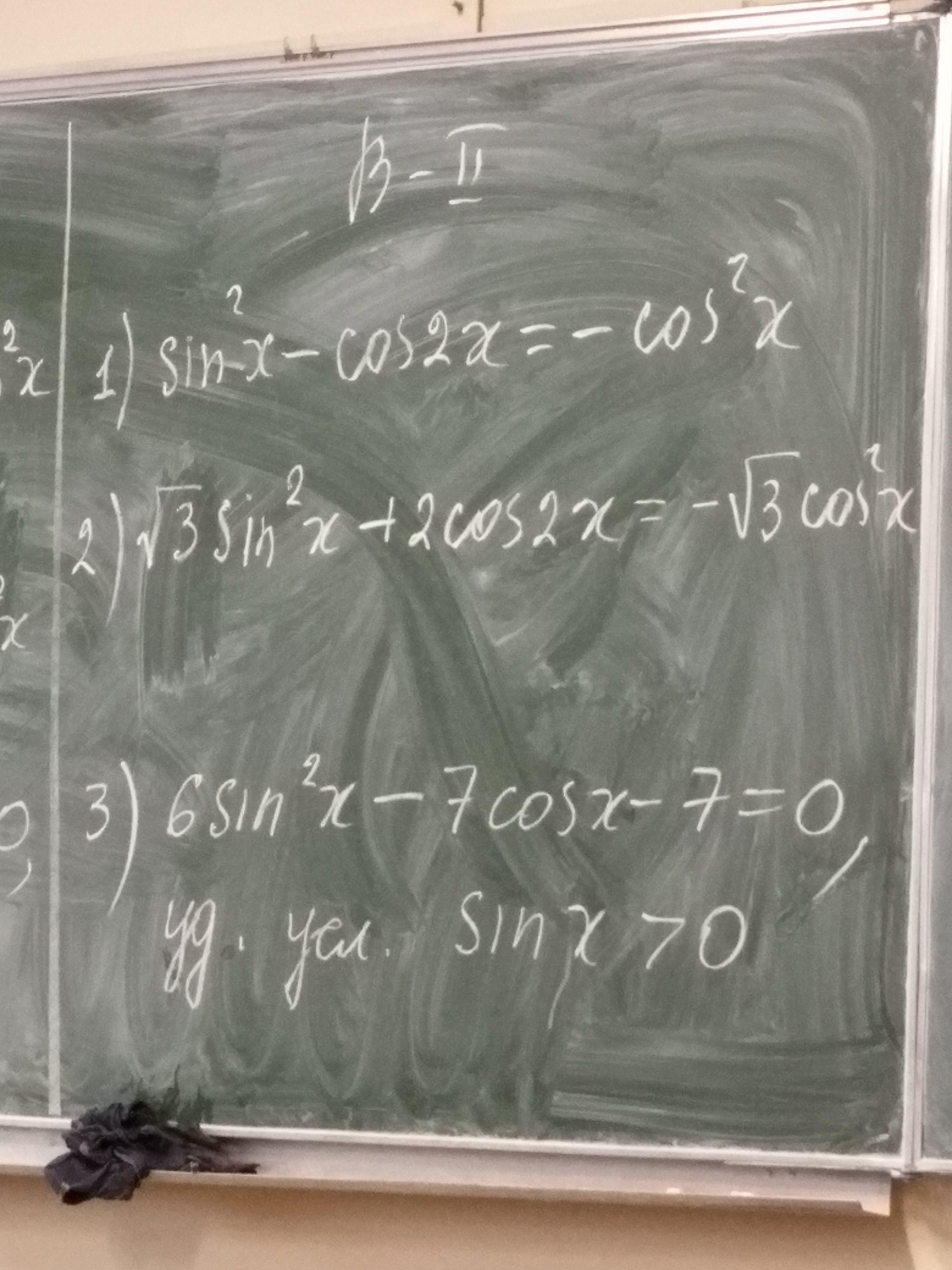
Ответы
Автор ответа:
1
1) Sin²x - Cos2x = - Cos²x
(Sin²x + Cos²x) - Cos2x = 0
1 - Cos2x = 0
Cos2x = 1
2x = 2πn, n ∈ z
x = πn , n ∈ z
2) √3Sin²x + 2Cos2x = - √3Cos²x
(√3Sin²x + √3Cos²x) + 2Cos2x = 0
√3(Sin²x + Cos²x) + 2Cos2x = 0
√3 + 2Cos2x = 0
2Cos2x = - √3
3)6Sin²x - 7Cosx - 7 = 0
6(1 - Cos²x) - 7Cosx - 7 = 0
6 - 6Cos²x - 7Cosx - 7 = 0
- 6Cos²x - 7Cosx - 1 = 0
6Cos²x + 7Cosx + 1 =0
- 1 ≤ Cosx ≤ 1
1) Cosx = - 1
x = π + 2πn , n ∈ z
Не подходит, так как Sinx > 0
kotodz333:
Огромное спасибо!
А зачем они здесь нужны?
К сожалению,я не знаю,но у нас их записывают,к сожалению не могу продемонстрировать. Возможно ли перейти в личные сообщения?
Можно
я к сожалению не могу с вами связаться, можно вы мне напишите? Прошу прощения за беспокойство
Если нужно найти решения уравнения на каком- то промежутке, то их можно искать на окружности. А у Вас задания, в которых нужно просто решить уравнения.
Спасибо огромное! Теперь всё ясно
Пожалуйста
https://znanija.com/task/32425970
помогите пожалуйста
Похожие вопросы
Предмет: Литература,
автор: Kunikidushka
Предмет: Математика,
автор: alishakirova21
Предмет: Русский язык,
автор: nghghghg
Предмет: Математика,
автор: ALINAMEI911
Предмет: Биология,
автор: 9Оля9