Question

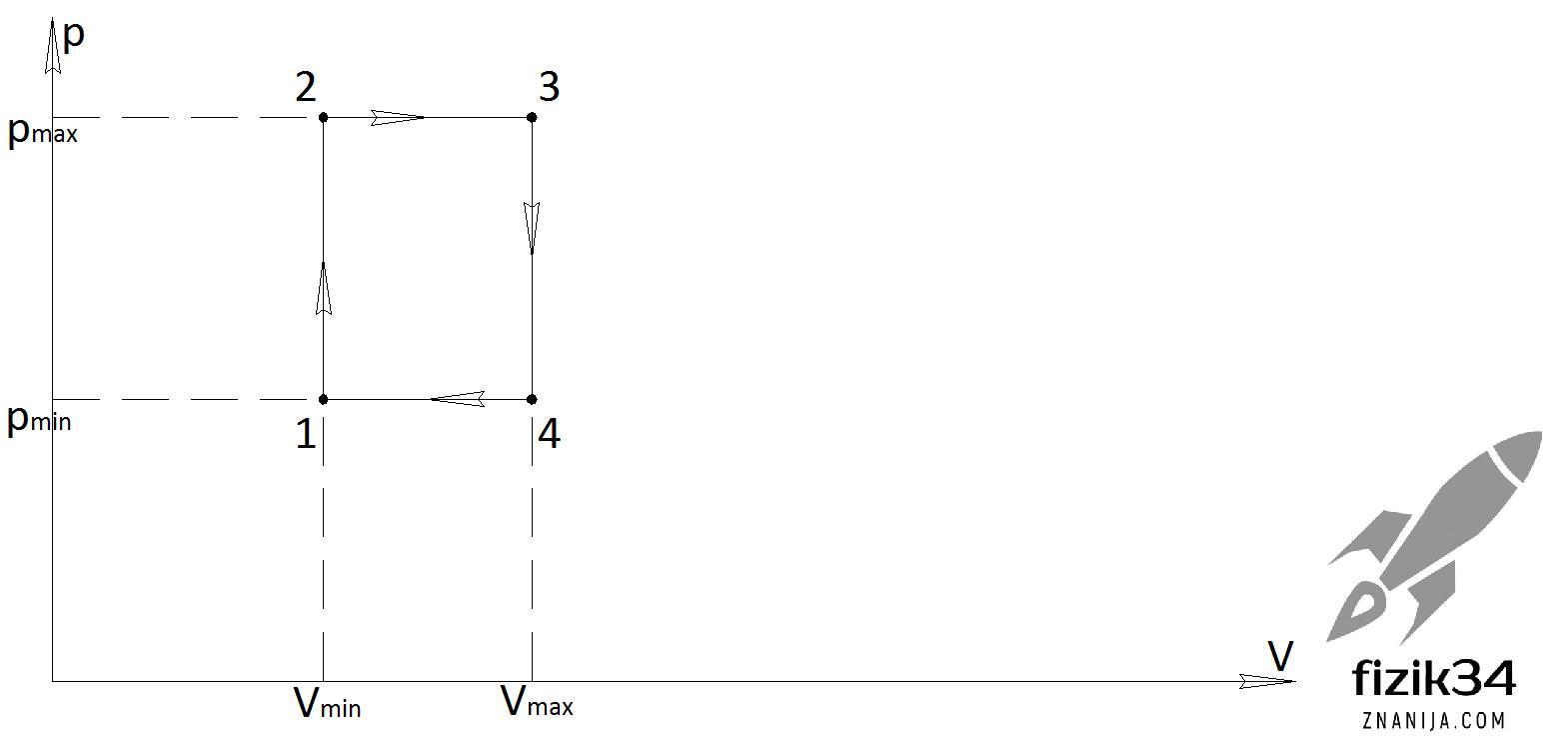
1 моль гелия совершает цикл, состоящий из двух изохор и двух изобар. Максимальное давление в цикле в 2 раза больше минимального, а максимальный объем в 1.5 раза больше минимального. определите в процентах коэффициент полезного действия цикла.

Answer 1

Ответ: 12.5%

Объяснение:

Параметр химического количества ве-ва - лишний

Дано:

$k = \dfrac{p_{\max}}{p_{\min} } = 2$

$n = \dfrac{V_{\max}}{V_{\min}} = 1.5$

Найти: η

Решение:

Начертим данный газовый цикл в координатах pV (см. приложение)

Итак, мы знаем что коэффициент полезного действия газового цикла можно определить как

η = A/Q

Где A - энергия затраченная на полезную работу в ходе всего цикла

Q - полная энергия переданная системе в ходе всего цикла

Полезную работу в ходе всего замкнутого цикла определим из соображений, что она численно равна площади полученной фигуры на графике в координатах pV

Так как в ходе газового процесса описного в условии у нас получиться прямоугольник, то

$A = (p_{\max} - p_{\min} )(V_{\max} - V_{\min})$

Т.к. $p_{\max}=kp_{\min}$, а $V_{\max}=nV_{\min}$, то

$A = (kp_{\min} - p_{\min})(nV_{\min} - V_{\min}) = p_{\min}V_{\min}(k - 1)(n - 1)$

Теперь определим полную энергию переданную системе в ходе всего цикла. Для этого обсудим на что расходовалось энергия в ходе газового цикла.

Итак, переход 1⇒2 - Изохорное нагревание. Входе этого перехода системе передавалась энергия затрачиваемая на увеличение внутренней энергии газа ΔU₁₂

Переход 2⇒3 - Изобарное нагревание. Входе этого перехода системе передавалась энергия затрачиваемая как на увеличение внутренней энергии газа ΔU₂₃, так и на совершение работы газом A₂₃

Переход 3⇒4 - Изохорное охлаждение. Входе этого перехода энергия извне не расходуется.

Переход 4⇒1 - Изобарное охлаждение. Входе этого перехода энергия извне не расходуется.

Итого Q = ΔU₁₂ + ΔU₂₃ + A₂₃

Или Q = ΔU₁₃ + A₂₃

Так, так как гелий одноатомный газ, то i=3, значит $\Delta U_{13} = \dfrac{3 }{2} \nu R \Delta T_{13}$

С учетом уравнения Менделеева-Клапейрона $\Delta U_{13} = \dfrac{3}{2} (p_{3} V_{3} -p_{1} V_{1} )$

Так как $V_{3} =V_{\max}$ и $p_{3} = p_{\max}$, а  $V_{1} =V_{\min}$ и $p_{1} = p_{\min}$, то

$\Delta U_{13} = \dfrac{3}{2} (p_{\max} V_{\max} -p_{\min} V_{\min} )$

Т.к. $p_{\max}=kp_{\min}$, а $V_{\max}=nV_{\min}$, то

$\Delta U_{13} = \dfrac{3}{2} (kp_{\min} nV_{\min} - p_{\min}V_{\min} )= \dfrac{3}{2}p_{\min} V_{\min} (kn -1)$

В свою очередь $A_{23} =p_{2} (V_{3} -V_{2} ) = p_{\max} (V_{\max} -V_{\min} )$

Т.к. $p_{\max}=kp_{\min}$, а $V_{\max}=nV_{\min}$, то

$A_{23} =kp_{\min} (nV_{\min} -V_{\min} )=kp_{\min}V_{\min} (n-1)$

Отсюда $Q = \dfrac{3}{2}p_{\min} V_{\min} (kn -1)+kp_{\min}V_{\min} (n-1)=p_{\min} V_{\min}(\dfrac{3}{2}(kn -1)+k(n-1))$

Спустя несколько преобразований $Q =\dfrac{ p_{\min} V_{\min}}{2} (5kn -2k-3)$

Итого $\eta = \dfrac{2p_{\min}V_{\min}(k - 1)(n - 1)}{p_{\min} V_{\min}(5kn -2k-3)}$

 $\eta = \dfrac{2(k - 1)(n - 1)}{5kn -2k-3}$

Окончательно получим $\eta = \dfrac{2(2 - 1)(1.5 - 1)}{5*2*1.5 -2*2-3}=0.125=12.5\%$