Предмет: Алгебра,
автор: СМЕРШ
Решите примеры во вложении:
Приложения:
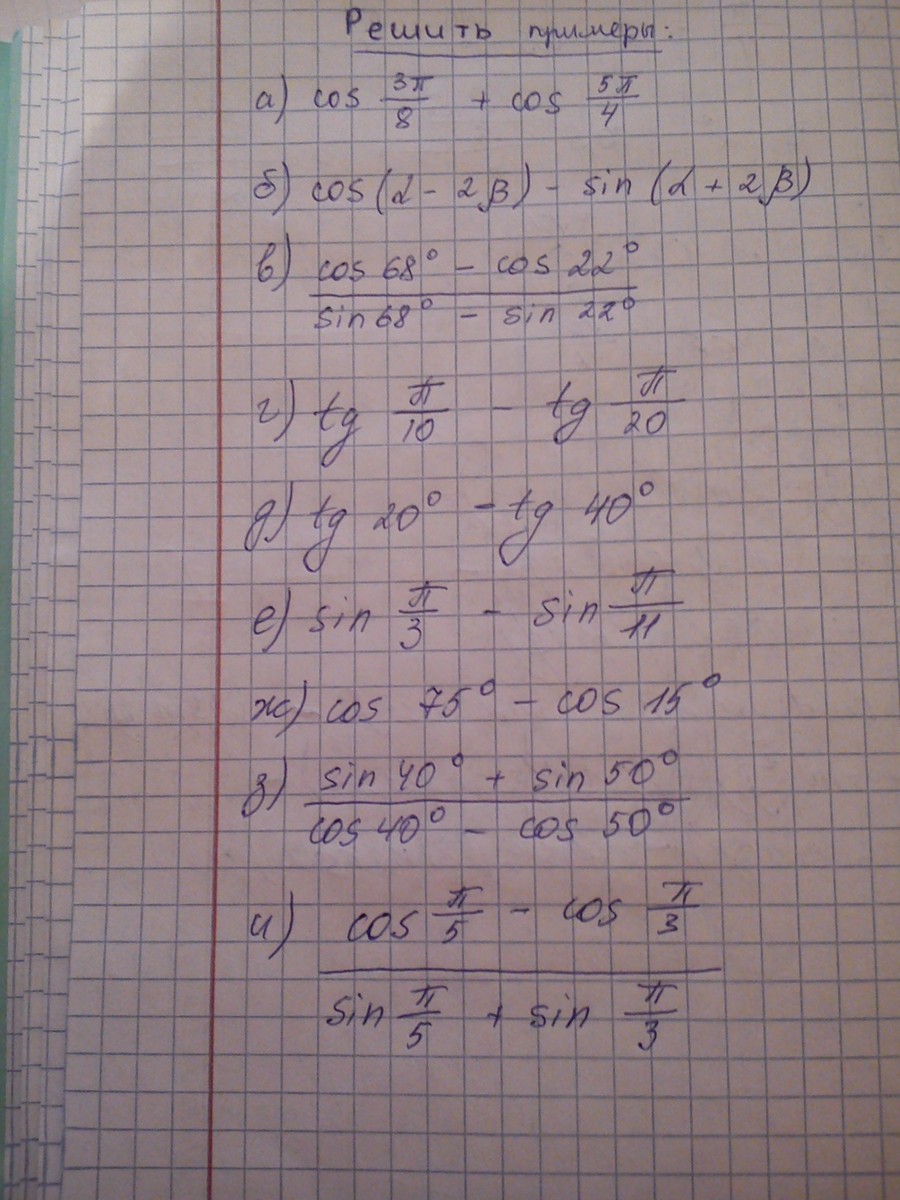
Ответы
Автор ответа:
0
либо оно равно
c)
d)
e)
g)
L)
f)
y)
Теперь если тебе нужно вычисления только в числах то работы чуть прибавится вычислим значения углов нестандартных!
Идея будет такая нам нужно найти либо
Геометрический будет легче разобраться ! Нарисуем прямоугольный треугольник , так что бы угол один был равен 36 гр другой 54 гр , тогда гипотенуза условно пусть будет равна 1, тогда соответствует такое соотношение !
Теперь выразим все
Подходит один угол так как это острый
Дальше легко просто подставьте !
Автор ответа:
0
в последнем если надо то можно вычислить выражение
Автор ответа:
0
Ок, если не трудно - сделай.
Похожие вопросы
Предмет: Физика,
автор: dsads40
Предмет: Литература,
автор: Аноним
Предмет: Биология,
автор: kokhLera
Предмет: Алгебра,
автор: alexsvi
Предмет: Информатика,
автор: iamwe