Question

При каком наибольшем значении а у уравнения |x2-8|x|+12|=a будет 6 корней?
С рисунком, если можно. Лучшее решение выберу обязательно)

Answer 1

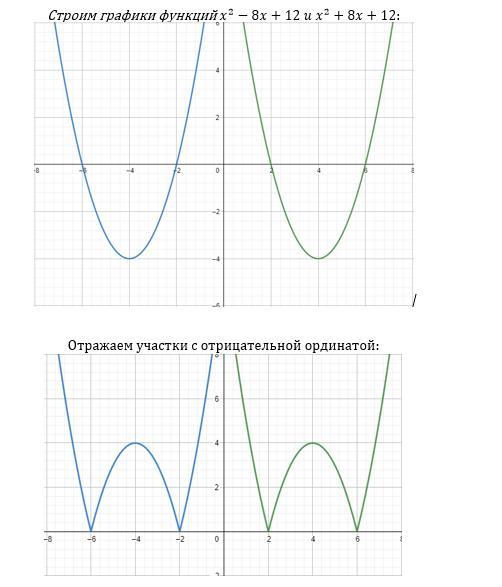
Решим данное уравнение графически. Рассмотрим левую часть уравнения. $x^{2}-8|x|+12=\left \{ {{x^{2}+8x+12,\;x\leq 0} \atop {x^{2}-8x+12,\;x>0}} \right.$; Затем отразим все те участки графика, расположенные ниже оси OX, относительно оси OX. В результате получим следующую картинку (https://www.desmos.com/calculator/rhzuktqgnp - график)

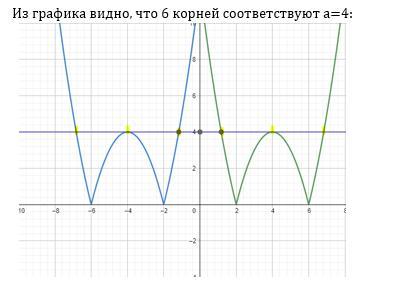
Из рисунка видно, что 6 корней (ровно) будет в единственном случае - когда a равно ординате вершины любой из парабол.

Найдем абсциссу вершины левой параболы:

$x_{0}=\frac{-8}{2}=-4$

Ордината равна $y_{0}=16-32+12=-4$, а после отражения равна 4.

Ответ: a=4

Answer 2

Ответ:

Не уверен, что правильно. Не дружу с параметрами, да еще плюс и модулями :). Если не секрет, откуда задача? Для ОГЭ тяжело, ибо там обычно одинарные модули, для ЕГЭ же легко.

Объяснение: