Question

Найдите площадь фигуры, ограниченную графиком функции.

f(x)= -x^2+3x-2 и осью абсцисс.

Спасибо заранее!

Answer 1

площадь под графиком функции, есть определенный интеграл:

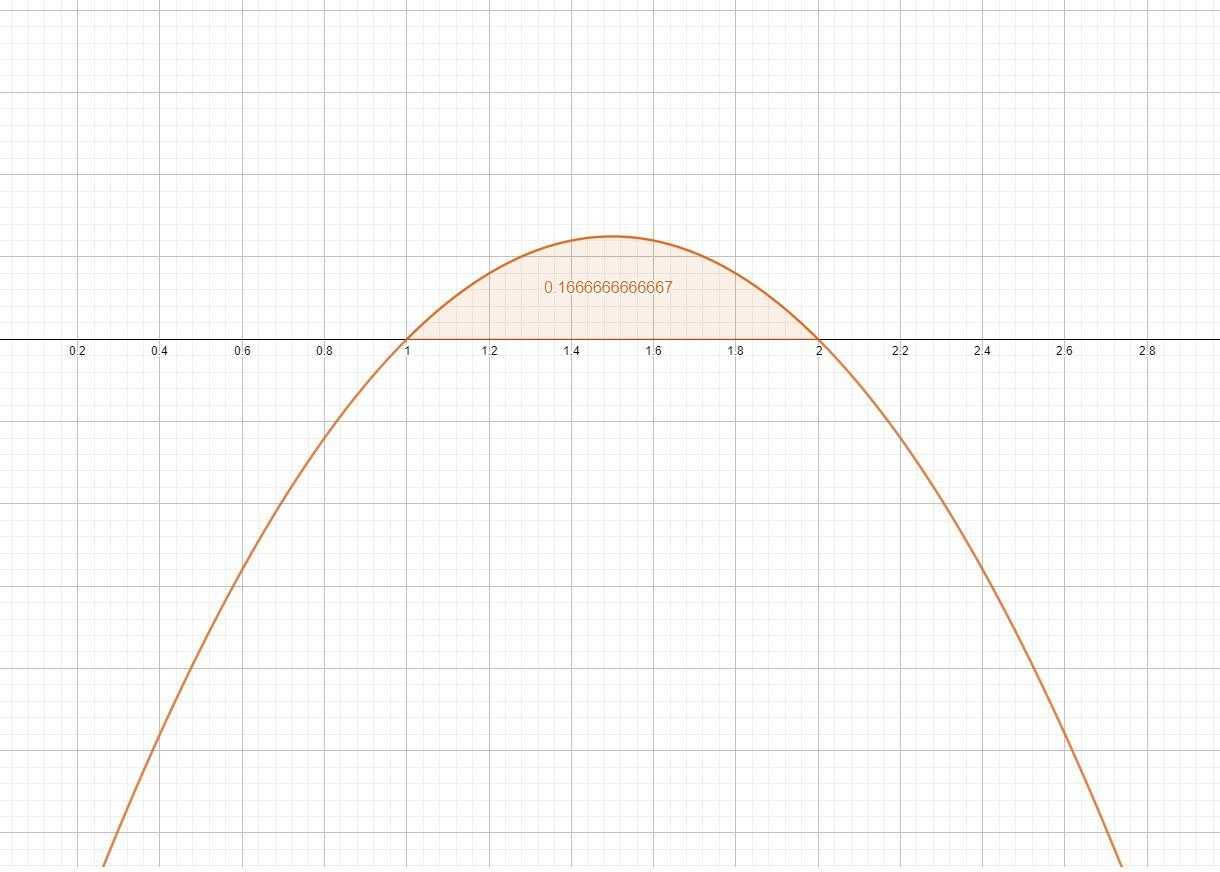
-x^2+3x-2 -это парабола с ветвями вниз и корнями, которая пересекает ось абсцисс в точках 2 и 1 (по теореме виета) см. рисунок.

$\int\limits^2_1 {-x^2+3x-2} \, (dx) =-\frac{x^3}{3}+\frac{3x^2}{2}-2x  |[1;2]=\\=(-\frac{8}{3}+6-4 )-(-\frac{1}{3}+\frac{3}{2}-2)=\\=(-\frac{2}{3} )-(-\frac{5}{6} )=\frac{5-4}{6}=\frac{1}{6}$

Ответ (1/6)

-------------------------

Ты в 10 классе интегралы решаешь или тебя заставили под конец 11?