Предмет: Математика,
автор: readandwatch112
Окружность, вписанная в равнобедренный треугольник ABC, касается его боковых сторон в точках E и F. Найдите периметр треугольника ABC, если его основание равно AC=12, а отрезок EF=3.
mathgenius:
AE=x (6+x)/x=12/3=4 6+x=4x x=2 P=12+2*(6+2)=28
Ответы
Автор ответа:
2
Ответ: 28
Пошаговое объяснение:
Пусть окружность касается основания в точке M,тогда из равенства отрезков касательных:
BM=MC=BE=CF=12/2=6.
Треугольник AEF подобен ABC, тк из за симметрии треугольника ABC и симметрии вписанной в него окружности EF параллельно AB. Пусть AB=x
x/(x-6)=12/3=4
x=4*(x-6)
x=4x-24
3x=24
x=8
P=2x+12=16+12=28
Приложения:
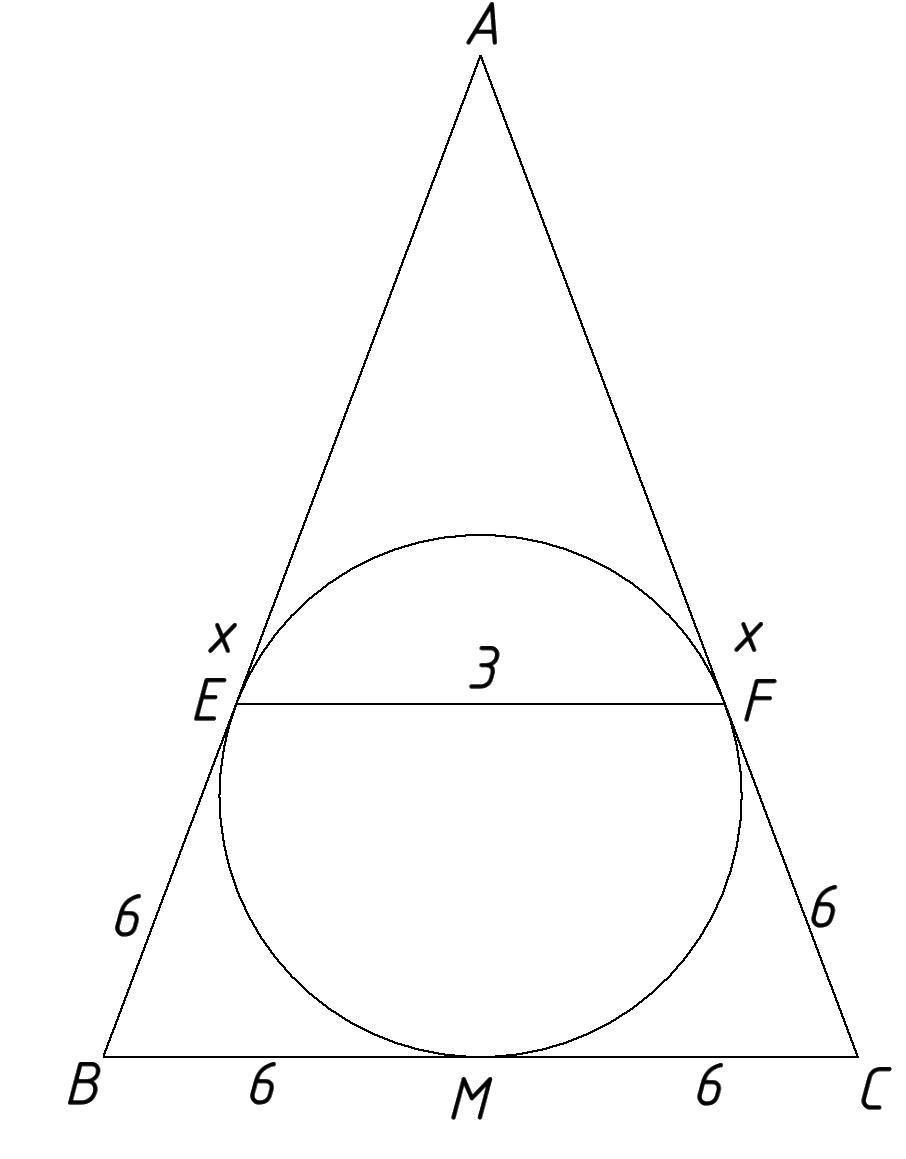
EF параллельно BC (описка)
Автор ответа:
1
АК = КС = АЕ = FC = 6 см как отрезки кассательных, проведённых к окружности с одной точки.
Пусть BF = EB = x см, тогда АВ = ВС = 6 + х см.
ΔАВС ~ ΔEBF (по основной т. подобия), отсюда имеем:
EF/АC = EB/AB;
3/12 = x/(6 + x);
3(6 + x) = 12x;
18 + 3x = 12x;
9x = 18;
x = 2.
Имеем: BF = EB = 2 см; АВ = ВС = 6 + 2 = 8 см; Р = АВ + ВС + АС = 2·8 + 12 = 16 + 12 = 28 см.
Ответ: 28 см.
Приложения:
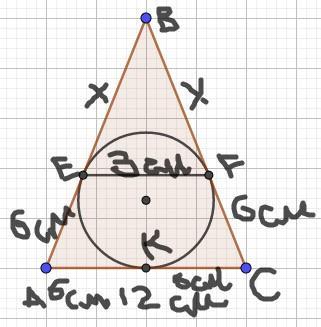
что то у вас пошло не так
Да, выижу опечатку. Сейчас исправлю
Похожие вопросы
Предмет: История,
автор: mynamejhon
Предмет: Биология,
автор: texbos
Предмет: Английский язык,
автор: Ghiwq
Предмет: Математика,
автор: iuliyasamoilic