Предмет: Математика,
автор: vsmirnov900
Решите систему уравнений пожалуйста. 10 баллов!!!
Приложения:
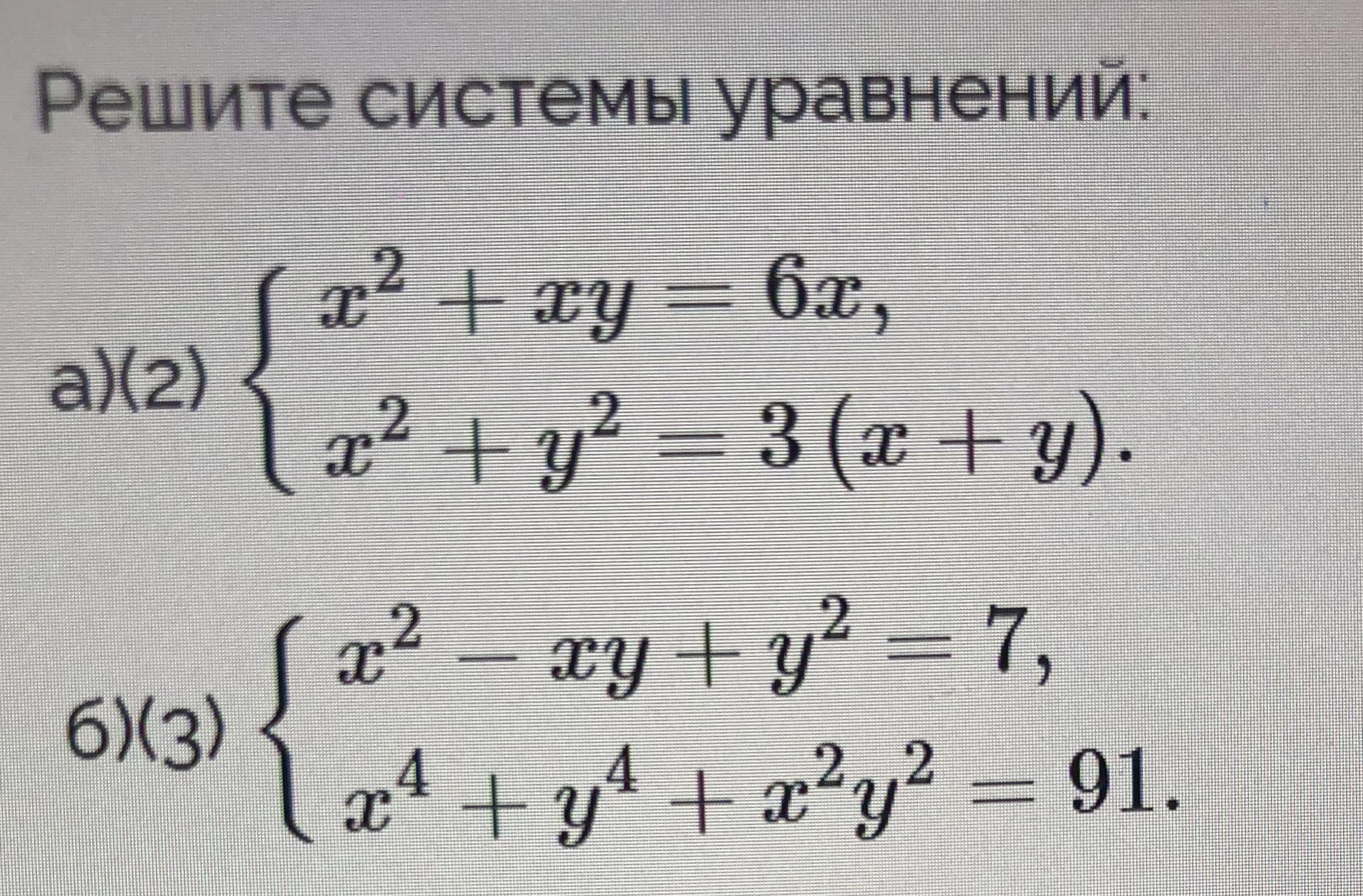
mathgenius:
в 1 легко x*(x+y-6)=0 , Рассматриваем два варианта. 2) Преобразуем первое уравнение так: x^2+y^2=7+xy , возводим в квадрат: x^4+y^4+2x^2*y^2= (7+xy)^2 x^4+x^2*y^2+y^4= (7+xy)^2- (xy)^2 (7+xy)^2- (xy)^2 =91 . xy=t . Найде xy , сразу находим x^2+y^2. Ход решения рассказал. Дальше сами действуйте
Расписывать лень
Ответы
Автор ответа:
1
1)
{ x^2 + xy = 6x
{ x^2 + y^2 = 3(x+y)
При х = 0 1-ое уравнение становится 0 = 0, 2-ое уравнение становится
0 + y^2 = 3(0 + y)
y^2 = 3y
y1 = 0; y2 = 3
Решения: (0; 0); (0; 3)
При х ≠ 0 делим 1-ое уравнение на х.
{ x + y = 6
{ x^2 + y^2 = 3(x+y) = 3*6 = 18
x^2 + (6 - x)^2 = 18
x^2 + x^2 - 12x + 36 = 18
2x^2 - 12x + 18 = 0
Делим все на 2.
x^2 - 6x + 9 = 0
(x - 3)^2 = 0
x = 3
y = 6 - x = 6 - 3 = 3
Решение: (3; 3)
2) Решение на рисунке.
Приложения:
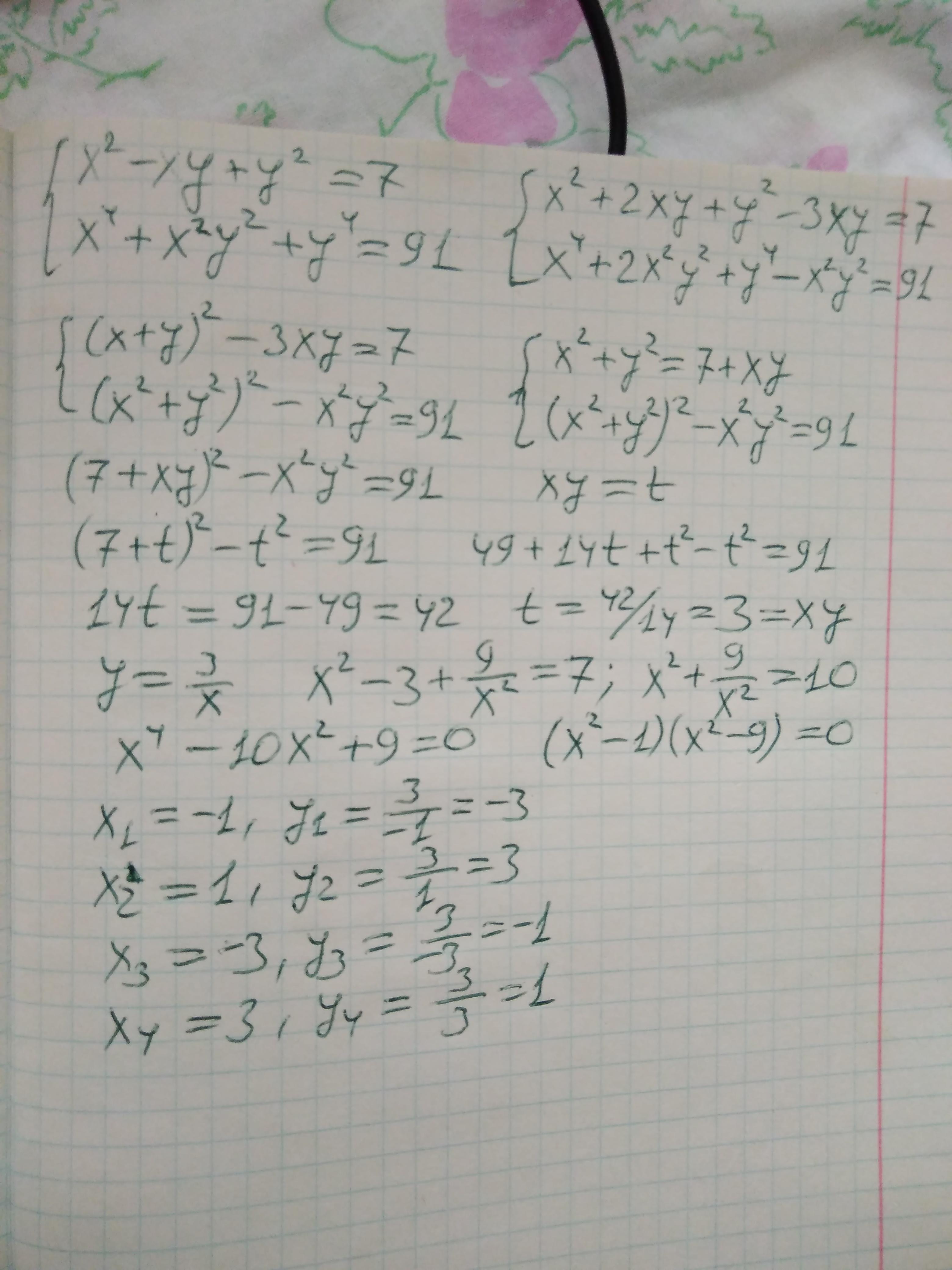
А 2 знаете как решить?
я написал в комментарии ход решения
дальше дело техники
решать квадратные уравнения
Ок, попробую
Спасибо
Похожие вопросы
Предмет: Математика,
автор: alzrostufaiden
Предмет: Геометрия,
автор: lordpffh1gg
Предмет: Физика,
автор: narutoibodalove
Предмет: Математика,
автор: hieri1
Предмет: Обществознание,
автор: hxjdhdvsv