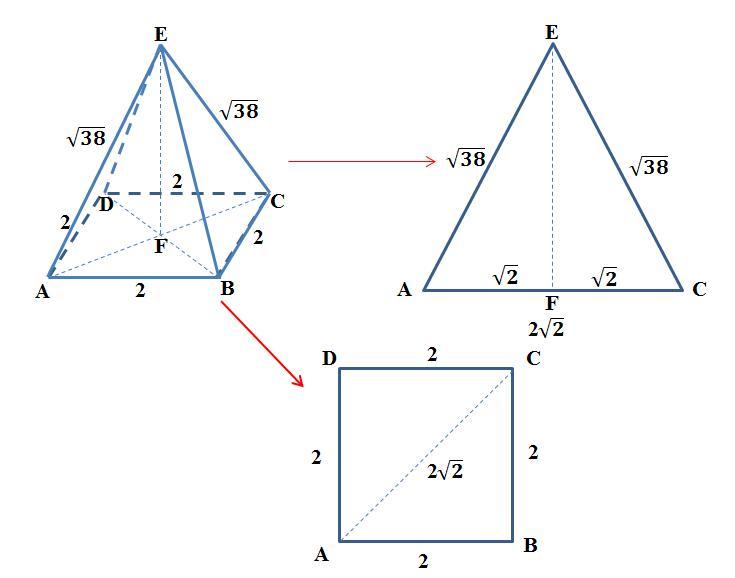
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 2, а боковое ребро равно √38
Ответы
Дано:
SABCD - прав. пирамида
ABCD - основание (квадрат)
AB = 2
SD = √38
Найти:
V - ?
Решение:
(см. рисунок)
BD = AB√2 = 2√2 (диагональ квадрата со стороной 2)
OD = BD / 2 = √2
Из ΔSOD (∠O = 90°) по теореме Пифагора получаем:
SD² = OD² + SO²
SO² = 38 - 2
SO² = 36
SO = √36 = 6
V = 1/3 · Sосн · SO = 1/3 · 2² · 6 = 8
Ответ:
V(пирамида) = 8 (куб. ед.)
Объяснение:
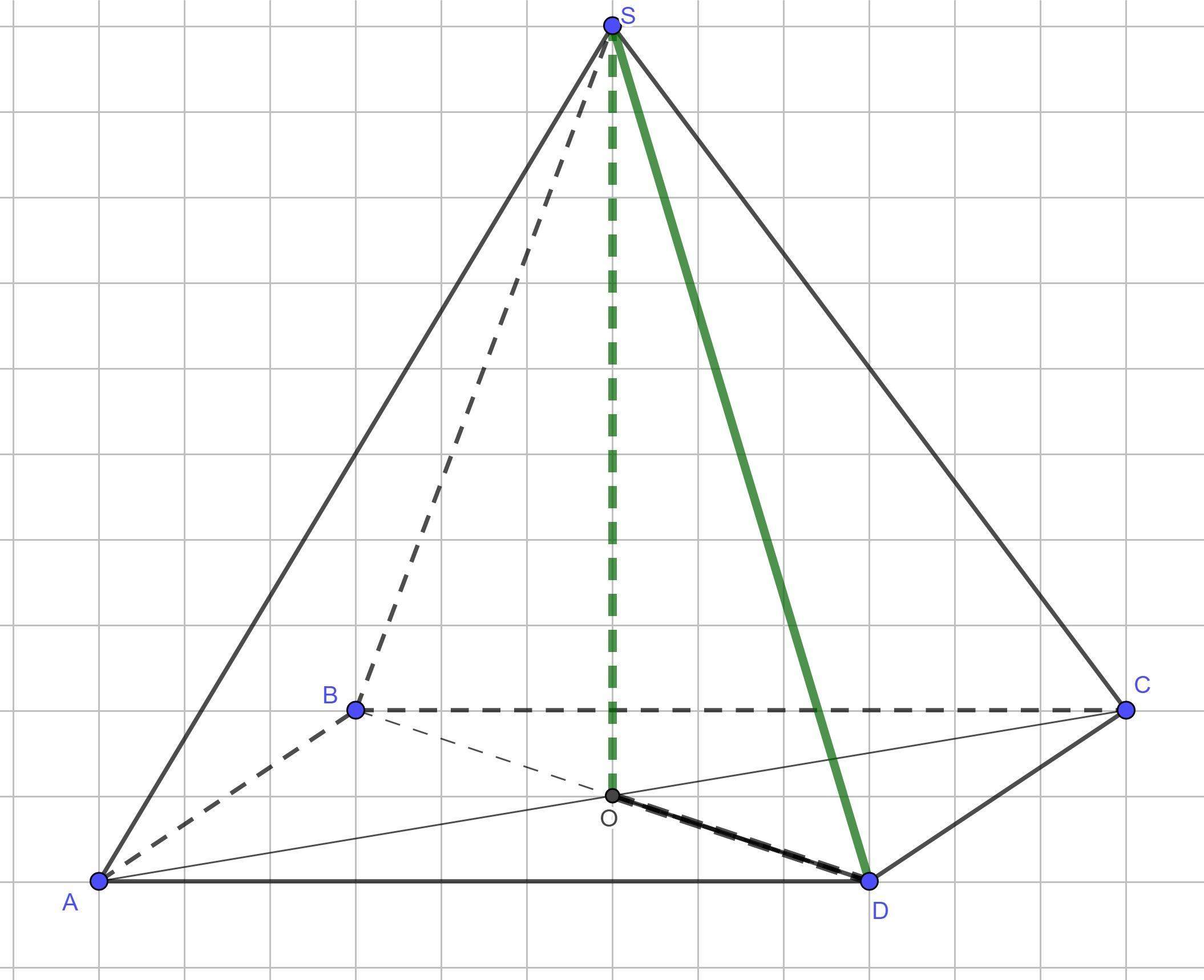
Дано (см. рисунок):
S(ABCD) – правильная пирамида
ABCD – основание
AB = BC = CD = DA = 2
AE = BE = CE = DE =√38
Найти: V(пирамида)
Решение:
Объём пирамиды определяется по формуле
V(пирамида) = 1/3 • S(ABCD) • h.
Так как пирамида является правильной, то в её основании лежит правильный четырёхугольник – квадрат ABCD со сторонами AB=BC=CD=DA=2, площадь которого равна S(ABCD) = AB²=2²=4.
Далее найдём неизвестную высоту пирамиды h=EF.
Рассмотрим прямоугольный треугольник ABC (здесь ∠B прямой, так как является углом квадрата ABCD). По теореме Пифагора
AC²=AB²+BC²=2²+2²=4+4=8 или AC=√8.
По свойству квадрата диагонали точкой пересечения делятся пополам, следовательно,
AF=FC=AC/2=(√8)/2=√(8/4) = √2.
Высота пирамиды EF перпендикулярна к плоскости основания ABCD, а также ко всем прямым, лежащим в этой плоскости. В частности, EF⊥AF, поэтому треугольник AFE является прямоугольным. Снова применим теорему Пифагора, согласно которой AE²=AF²+EF².
Отсюда
h²=EF²=AE²–AF²=(√38)²–(√2)²=38–2=36=62 или h=6.
Подставляя найденные значения S(ABCD) = 4 и h=6, получим искомый объём пирамиды
V(пирамида) = 1/3 • 4 • 6 = 8 (куб. ед.).