Предмет: Алгебра,
автор: qwertyuisdf18523sf
помогите пожалуйста даю 30 баллов
Приложения:
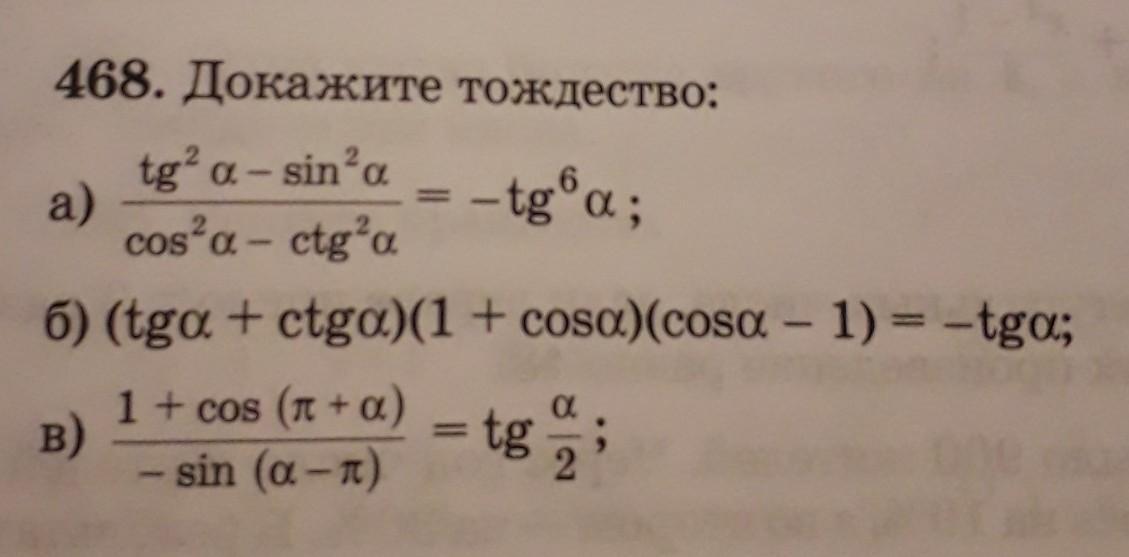
Ответы
Автор ответа:
1
Тождество доказано
- tgα = - tgα
Тождество доказано
Тождество доказано
Похожие вопросы
Предмет: Қазақ тiлi,
автор: xaxaxaxxaxaxxaax
Предмет: Геометрия,
автор: elizavetalobareva72
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: милимисса