Три одинаковые окружности радиуса r попарно касаются друг друга. Найти стороны треугольника, образованного внешними касательными к этим окружностям.
Ответы
Ответ:
Стороны искомого треугольника равны 2r(1+√3).
Объяснение:
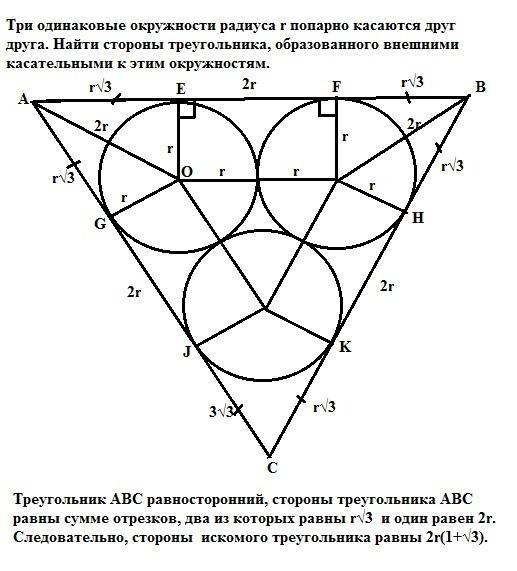
АВ, АС и ВС - касательные к попарно касающимся окружностям радиуса r.
Отрезки AE=AG, CJ=CK, BF=BH как отрезки касательных, проведенных к окружности из одной точки. Отрезки EF=GJ=KH= 2r как противоположные стороны прямоугольников, образованных радиусами окружностей, проведенных в точки касания и отрезками, соединяющими центры касающихся окружностей, равными сумме радиусов этих окружностей. Таким образом, треугольник АВС равносторонний, так как его стороны равны сумме равных отрезков.
Углы равностороннего треугольника равны 60°.
Рассмотрим треугольник АОЕ. Угол ЕАО = 30° (так как АО - биссектриса по свойству отрезка, соединяющего общую точку касательных к окружности с центром этой окружности). Катет против угла 30° равен половине гипотенузы => AO=2r => AE = r√3.
Итак, стороны треугольника АВС равны сумме отрезков, два из которых равны r√3 и один равен 2r. Следовательно, стороны искомого треугольника равны 2r(1+√3).
Ответ:
Объяснение: решение в файле
