Question

Сформулируйте и докажите чему равен периметр треугольника,
образованного двумя касательными из одной точки и касательной,
проведенной к этой окружности через точку внутренней дуги.
(8 класс)

Answer 1

Ответ:

Объяснение:

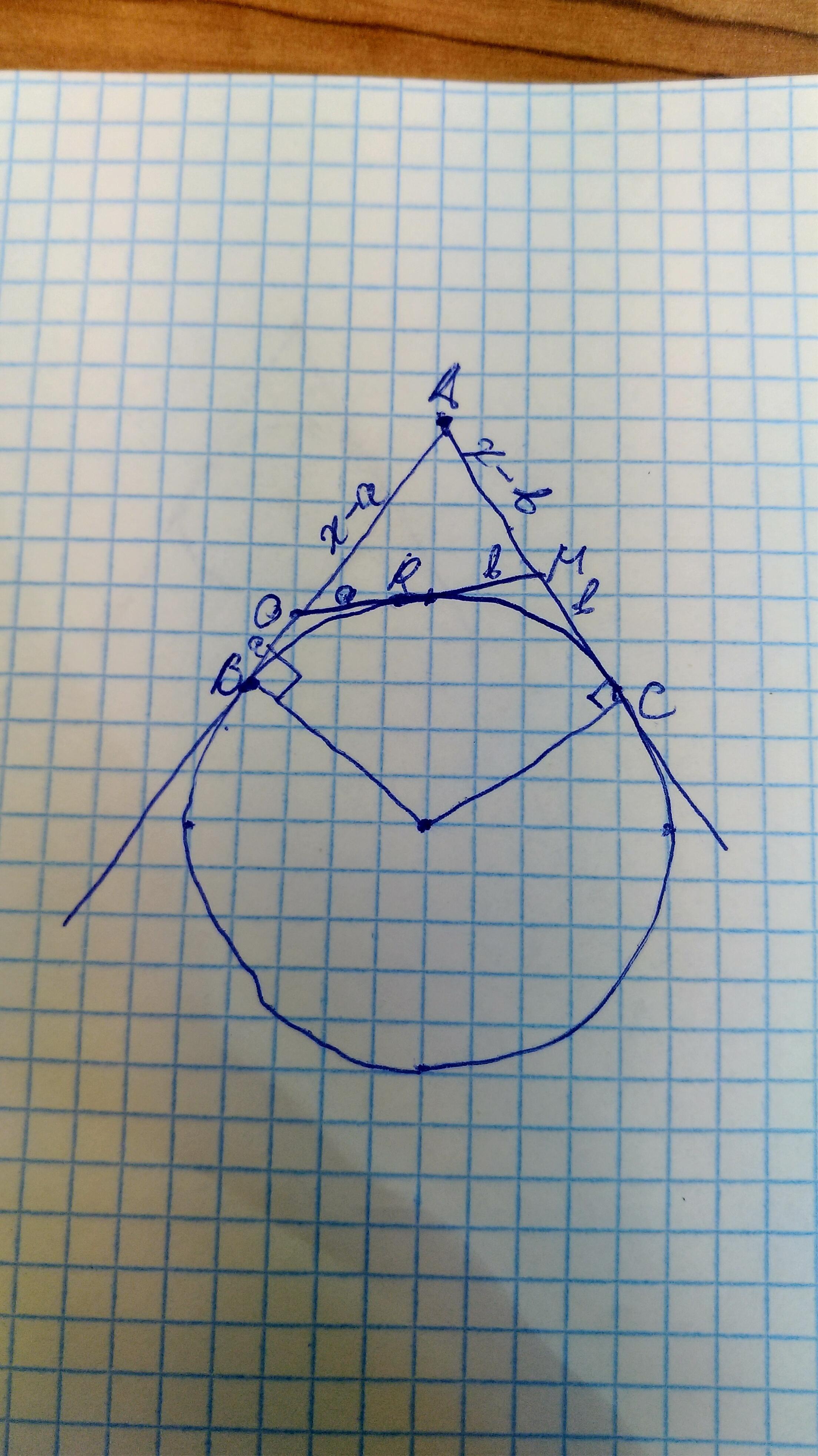
Пусть длинна касательной: AB=AC=x. Из равенства отрезков касательных следует очевидное равенство:

OB=OR=a. MR=MC=b. Откуда:

AO=x-a ; AM=x-b; OM=a+b

Откуда P(ABM)=x-a +x-b +a+b=2x. Таким образом периметр такого треугольника равен удвоенной длинне касательной.

Answer 2

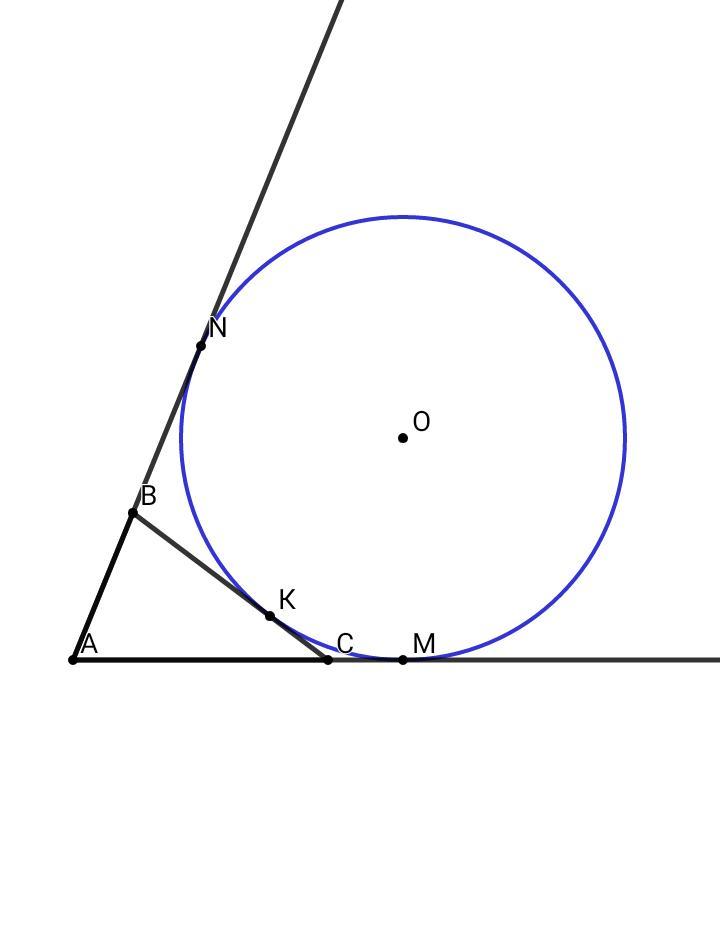
Отрезки касательных к окружности, проведенных из одной точки, равны

AN = AM , BN = BK , CM = CK

P abc = AB + AC + BC = AB + AC + (BK + CM) = AB + AC + (BN + CM) = (AB + BN) + (AC + CM) = AN + AМ = AM + AM = 2•AM

Значит, периметр треугольника, образованного двумя касательными из одной точки и касательной, проведённой к этой окружности через точку внутренней дуги, равен удвоенному бо'льшему отрезку его касательной