Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Смежные углы равны.
3) Все диаметры окружности равны между собой.
Если утверждений несколько, запишите их номера в порядке возрастания.
Ответ:
Ответы
Проанализируем каждое утверждение.
1) Неравенство треугольника гласит: "Каждая сторона треугольника меньше суммы двух других сторон".
Составим неравенства и проверим их на верность -
4+1 > 2 ⇒ 3 > 2.
4+2 > 1 ⇒ 6 > 1.
2+1 > 4 ⇒ 3 > 4 - это неверное неравенство, сторона треугольника не может быть больше суммы двух других сторон, следовательно, такого треугольника не существует.
Ответ: утверждение 1 верно.
2) Смежные углы, конечно же, могут быть равны (когда каждый из них равен по 90°).
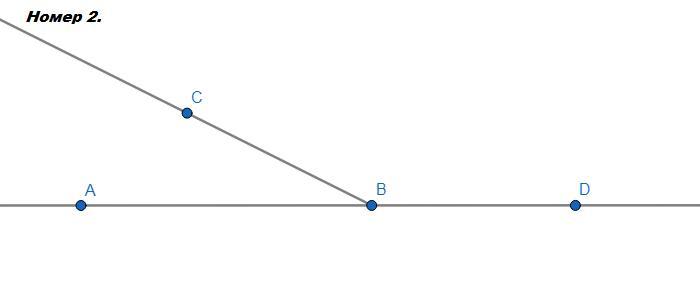
Рассмотрим какие-нибудь смежные углы, пусть один из них будет тупой. (на картинке ∠CBD - тупой). Тогда какого вида будет ∠СВА?
Так как сумма смежных углов равна 180°, а тупой угол - это угол, градусная мера которого больше 90°. Если ∠CBD = 91°, тогда ∠СВА = 180°-∠CBD = 180°-91° = 89° - острый угол. (Можете сами поэкспериментировать, угол, смежный с тупым углом - всегда острый угол). Утверждение 2 не всегда может быть верным, так как острый и тупой угол не могут быть равны.
Ответ: утверждение 2 неверно.
3) Совершенно верно. Это одно из свойств окружности.
Ответ: утверждение 3 верно.
Ответ: 13.