Предмет: Геометрия,
автор: adamovichdariya
Помогите пожайлуйста!!!Сделать решение и рисунок! Если хотите можно писмено!!!
Радиус описанной окружности около равностороннего треугольника равен 6. Найдите сторону треугольника, радиус вписанной окружности и площадь треугольника.
Ответы
Автор ответа:
1
Ответ:
r = 3
a = 6√3
S = 27√3
Объяснение:
R = 6
В равностороннем треугольнике радиус вписанной окружности вдвое меньше радиуса описанной окружности.
r = R/2 = 6/2 = 3
По формуле радиуса описанной окружности:
R = aₙ/(2 * sin (180/n))
6 = aₙ/(2 * sin (60°))
sin (60°) = √3/2
6 = aₙ/(2 * √3/2)
6 = aₙ/√3
aₙ = 6√3
По формуле площади равностороннего треугольника:
S = (a²√3)/4
S = ((6√3)²√3)/4 = (108√3)/4 = 27√3
Приложения:
adamovichdariya:
Можно спросить как выглядить рисунок этого фигуры?
Как мне ее нарисовать?
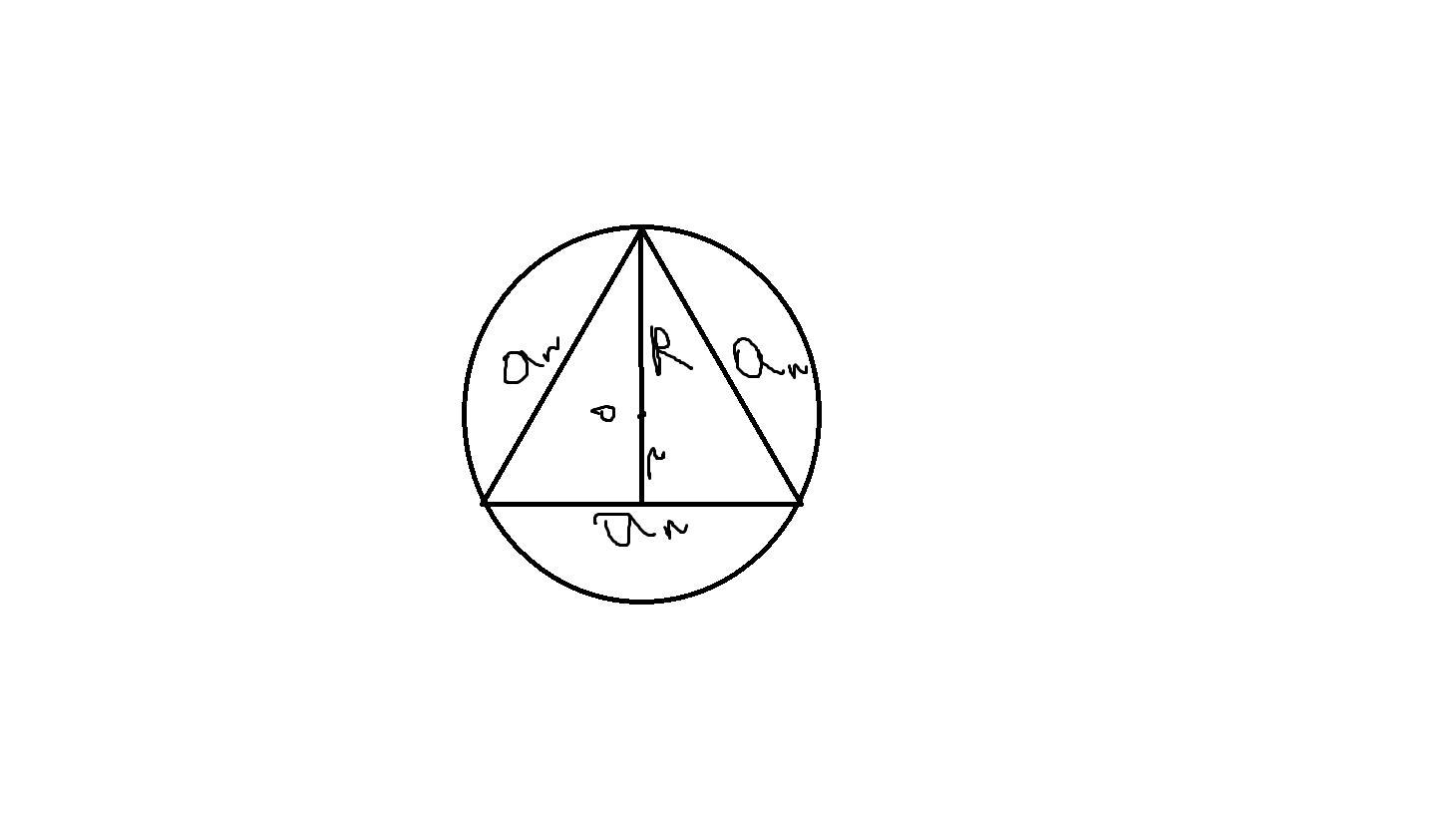
прикрепил фото. Там примерно так, нужно только подстваить значения и все
Спасибо
Похожие вопросы
Предмет: Английский язык,
автор: anya20090611koryakin
Предмет: Алгебра,
автор: lliza6326
Предмет: Қазақ тiлi,
автор: zhenya20112021
Предмет: Литература,
автор: karinanikolaev2
Предмет: Алгебра,
автор: Аноним