Question

Найдите высоту равнобедренного треугольника , проведенную к основанию, если основание равно 12 см, а угол при вершине треугольника равен 120∘

Answer 1

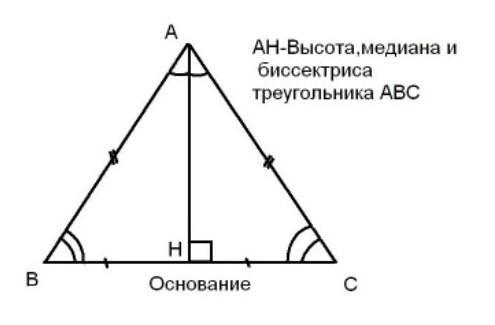
Высота,  проведенная к основанию, является и медианой, делит основание пополам, т.е. на две части по 6см, и биссектрисой, делит угол на две равные части по 60°; чтобы найти катет, прилежащий к углу 60°, т.е. высоту треугольника, надо 12*ctg60°=12*√3/3=4√3/cм/

Answer 2

Высота равнобедренного треугольника является медианой, поэтому ВН=НС=6 см, и помимо этого является и биссектрисой, поэтому угол ВАН=угол НАС=60 градусов.

Рассм. треуг. АВН: он прямоугольный, tgBAH=BH/AH; tg60=6/x;

$\frac{6}{x} = \sqrt{ 3} \\ x = \frac{6}{ \sqrt{3} } \\ x = 2 \sqrt{3}$

Ответ:

$2 \sqrt{3}$