Предмет: Алгебра,
автор: Bomjara228
Изменить порядок интегрирования и вычислить двойной интеграл

Ответы
Автор ответа:
1
Ответ: 2π√2
Объяснение:
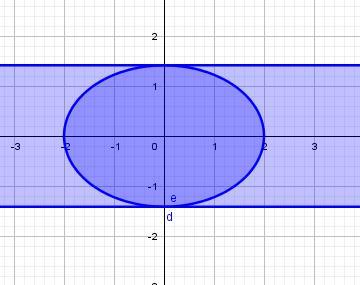
Найдем точки пересечения с осью ординат
x = 0: 4 - 2y² = 0 ⇔ y = ± √2
Приложения:
Bomjara228:
Спасибо большое, а что дальше получится, если вычислять двойной интеграл? Не могли бы еще с этим помочь...
Спасибо :З
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: margosha0453
Предмет: Математика,
автор: murmur270809
Предмет: Математика,
автор: 123daniel
Предмет: Математика,
автор: Аноним