Предмет: Геометрия,
автор: MonikaBeluchisss
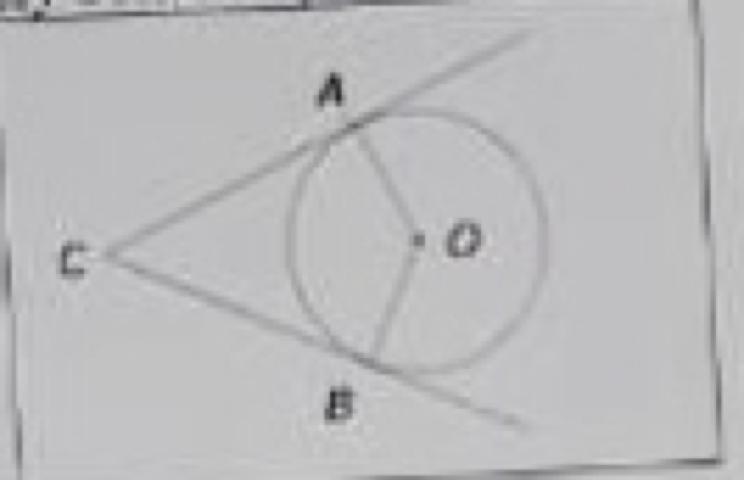
Две прямые касаются окружности с центром О в точках А и В и пересекаются в точке С. Найдите угол между этими прямыми,если <АВО=38(Определить вид треугольника АОВ, использовать свойство касательной(перпендикуляр. радиус) и определить углы АВС, найти величину искомого угла) 20 баллов
Приложения:
Ответы
Автор ответа:
15
Треугольник OAB равнобедренный так-как OA=OB как радиусы.
∠ABO=∠BAO=38°
значит на угол AOB=180-38-38=104°
------------------
Рассмотрим четырехугольник CABO, у него 2 прямых угла (OAC и OBC) и угол AOB=104°, Значит на угол ACB приходится: 360-90-90-104=76°
так как сумма углов четырехугольника=360 градусов.
------------
Остальные 2 угла (CBA и CAB) равны 90-38=52°
Ответ: угол между прямыми=76°
Похожие вопросы
Предмет: Геометрия,
автор: kirillkoval501
Предмет: Математика,
автор: Fla3r
Предмет: Алгебра,
автор: kirillkalmyk123
Предмет: Математика,
автор: ученик1911
Предмет: Математика,
автор: karina052016