Предмет: Геометрия,
автор: Danystalker
Срочно помогите пожалуйста)
Приложения:
Ответы
Автор ответа:
1
Ответ:
Решение
Объяснение:
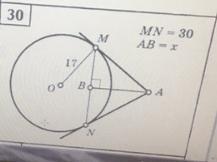
AM = AN (как касательные)
ΔAMN - равнобедренный, а значит AB - медиана:
BM = BN = MN/2 = 30/2 = 15
В ΔOBM ∠B = 90°. По теореме Пифагора:
OB² = OM² - BM²
OB = √(289 - 225) = √64 = 8
OB = 8
∠OMA = 90° (радиус к касательной)
Рассмотрим ΔOMA:
По теореме Пифагора:
AM² = OA² - OM²
AM = √(OA - 289)
OA = x + 8
AM = √((x + 8)² - 289)
Рассмотрим ΔABM:
∠ABM = 90° (по условию)
По теореме Пифагора:
AM² = AB² + MB²
AM = √(x² + 225))
Система:
AM = √((x + 8)² - 289)
AM = √(x² + 225))
Приравняем:
√((x + 8)² - 289) = √(x² + 225))
(x + 8)² - 289 = x² + 225
x² + 16x + 64 - 289 = x² + 225
16x = 550
x = 550/16 = 225/8 = 28,125
x = 28,125
Похожие вопросы
Предмет: Математика,
автор: cuverkalovroman
Предмет: Другие предметы,
автор: rujiktytry
Предмет: Математика,
автор: sskelsarova95
Предмет: Геометрия,
автор: naraker
Предмет: Обществознание,
автор: энже3