Предмет: Алгебра,
автор: 791312
Помогите решить,только с решением
90 баллов
Приложения:
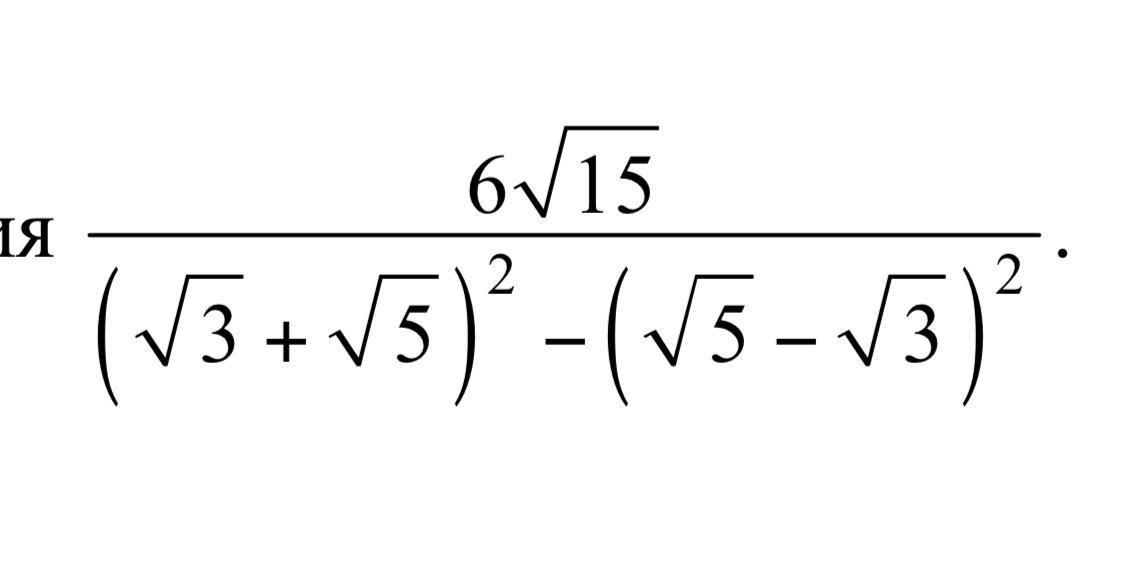
Ответы
Автор ответа:
0
Ответ: 3/2.
Объяснение:
Автор ответа:
1
Похожие вопросы
Предмет: Биология,
автор: gfrtn592
Предмет: Литература,
автор: dkuzmenko8795
Предмет: Математика,
автор: gosha98123476
Предмет: Математика,
автор: Nastya3783