Question

Вершины треугольника ABC делят описанную около него окружность на дуги AB, BC, CA, длины которых относятся как 3 : 4 : 5. Найдите радиус окружности, если меньшая из сторон треугольника равна 32.

Answer 1

Пусть меньшая из дуг будет 3x тогда остальные дуги=4x и 5x соответственно.

Составим уравнение:

3x+4x+5x=360°

x=30°

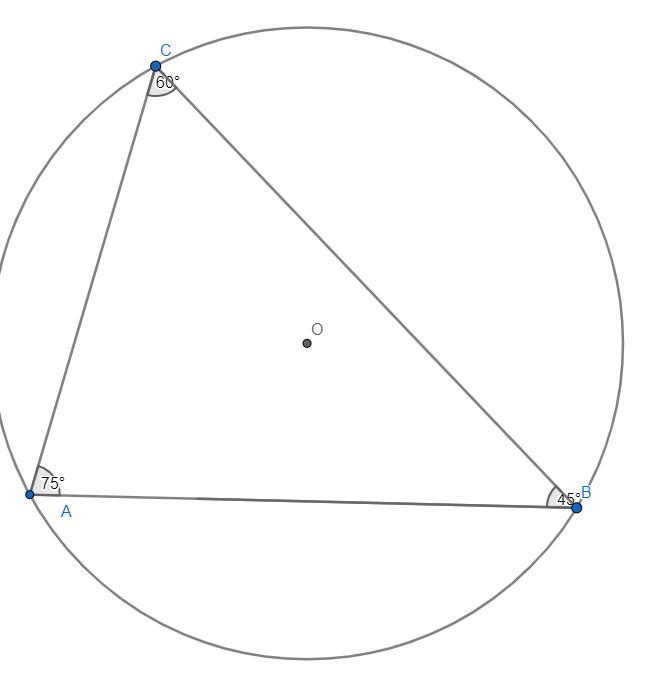
значит меньшая дуга=90°, а меньший угол (лежащий напротив меньшей стороны) треугольника=45°

--------------

Из теоремы синусов:

$\frac{a}{sin(\alpha )} =2R\\R=\frac{a}{2sin(\alpha)} =\frac{32}{2sin(45)}=16\sqrt{2}$

Ответ: $16\sqrt{2}$