Предмет: Геометрия,
автор: Elsh007
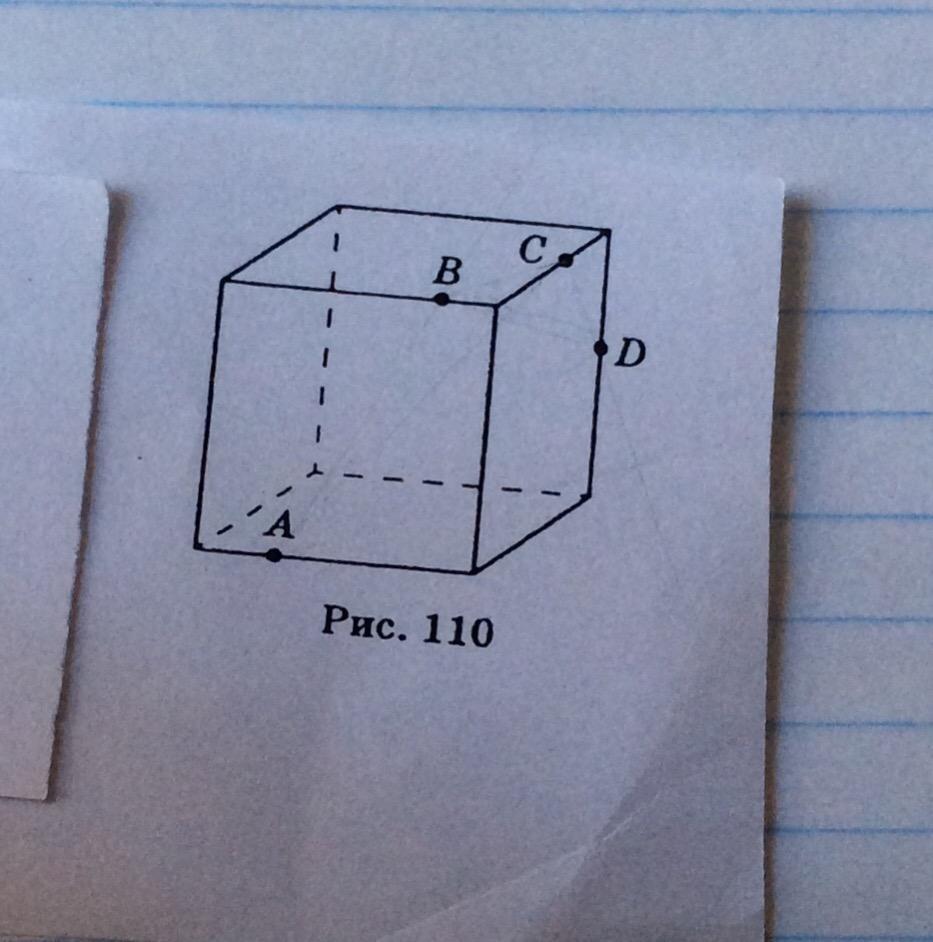
Точки A, B, C, D лежат на рёбрах изображённого куба. Определите, пересекаются ли отрезки AC и BD.
Приложения:
mathgenius:
Решение геометрическое? То есть проверить надо циркулем и линейкой?
Пытался алгебраически получить противоречие с применением неравенств,но тех неравенств что честно видно так сказать на глаз недостаточно для того чтобы поймать какое то противоречие
Для расстояний от точек до вершин кубов справедливо такое соотношение: 1-a/b=1/d-1/cd . Сторону куба считаем единицей длинны (равна 1). На глаз ,,честно'' можно видеть только такие неравенства: 0 1/2 ; c>1/2 к сожалению на их основе поймать какое то противоречие не удается
Ответы
Автор ответа:
0
Ответ:
AC∩BD=O
Объяснение:
построим сечение куба плоскостью, проходящей через точки A, B, C, D.
построение
1. прямая AD, точки A и D принадлежат одной грани
2. прямая ВС
3. прямая CD
4. прямая AK, AK||BC
5. прямая KD
6. пятиугольник ABCDK - искомое сечение
прямые AC и BD принадлежат плоскости ABCDK.
взаимное расположение прямых в плоскости:
а). прямые пересекаются
б). прямые параллельны
ответ: прямые AC и BD пересекаются
Приложения:
Похожие вопросы
Предмет: Химия,
автор: avrilmodi
Предмет: Алгебра,
автор: whazzy
Предмет: Литература,
автор: ruslanmatveevic
Предмет: Математика,
автор: MikaCarson12