Предмет: Математика,
автор: 19831986we
Решите систему линейных алгебраических уравнений
Тремя методами (метод Гаусса, метод Крамера,
Метод обратной матрицы)
Приложения:
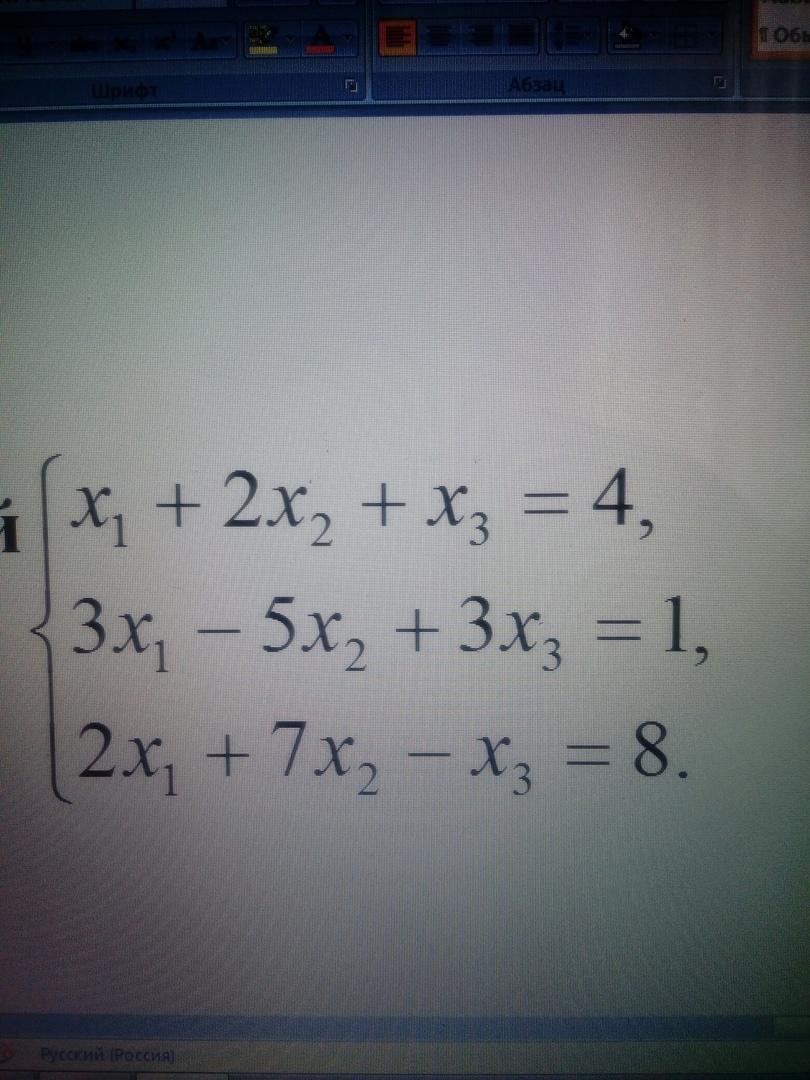
Ответы
Автор ответа:
2
Пошаговое объяснение:
1) Метод Гаусса:
2) Метод Крамера
3) Матричный метод
Похожие вопросы
Предмет: Биология,
автор: karma5740
Предмет: Математика,
автор: araxis7632
Предмет: Математика,
автор: makckuznetsov7198
Предмет: Геометрия,
автор: wotgameswot