Предмет: Математика,
автор: artemich7
Вычислить интеграл.
∫arctg 5x dx
Ответы
Автор ответа:
0
Пошаговое объяснение:
Интегрирование по частям.
Приложения:
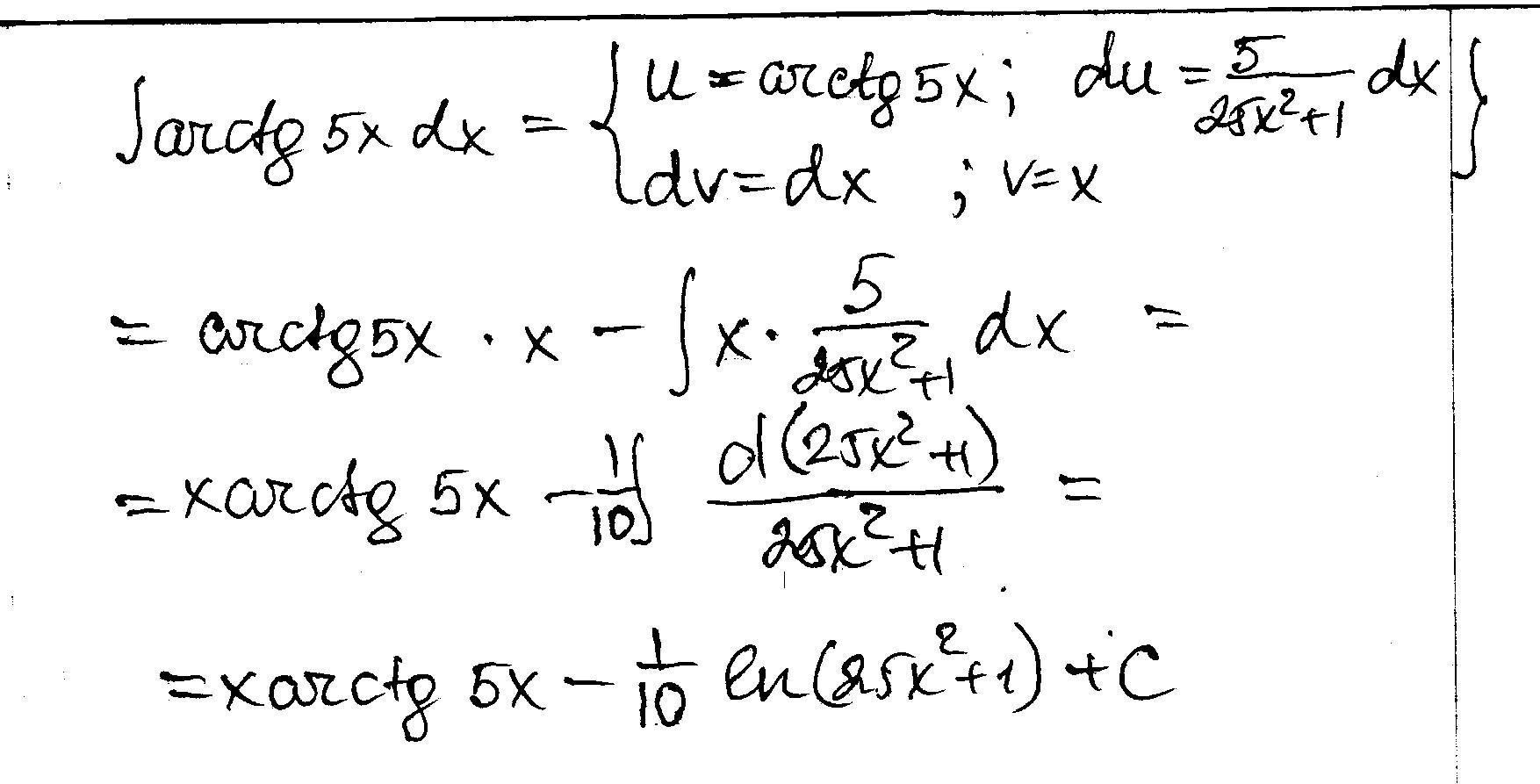
Автор ответа:
1
daniilzhulanov:
ууу спасибо помог
Похожие вопросы
Предмет: Математика,
автор: gulij5993
Предмет: Математика,
автор: kristy4939
Предмет: Математика,
автор: vikrehh9527
Предмет: Алгебра,
автор: ns100549