Question

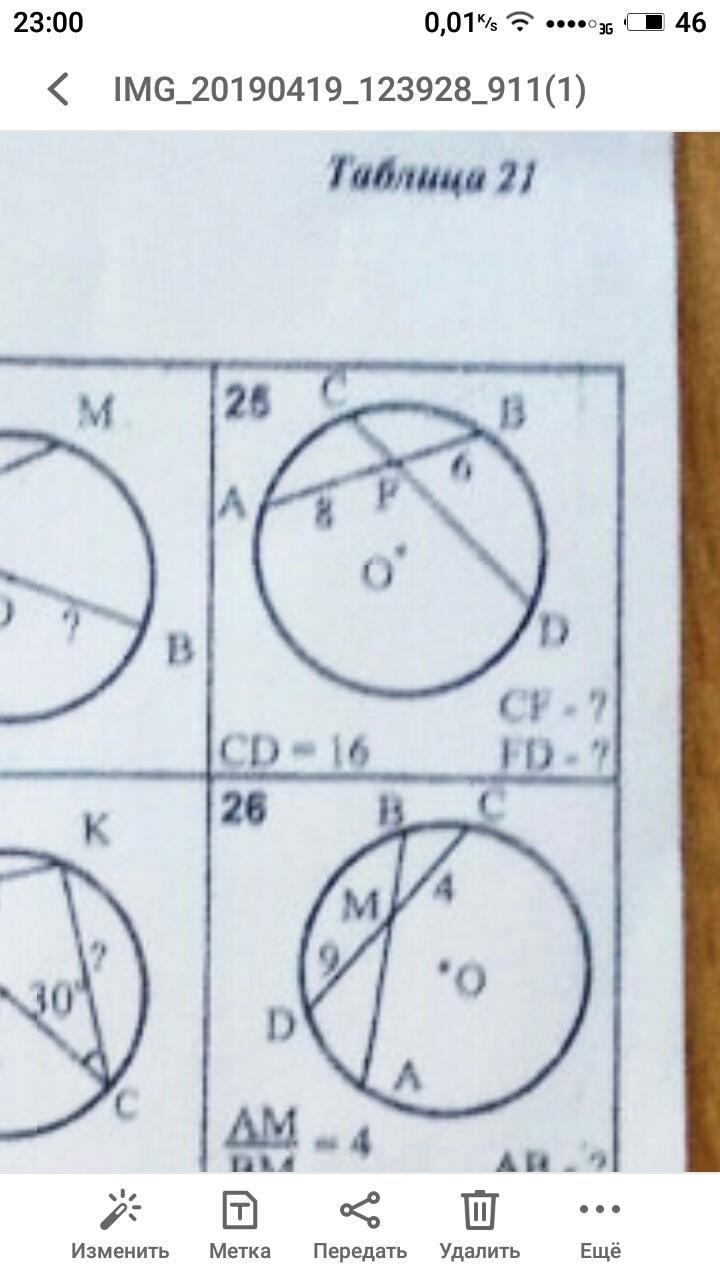
Две хорды AB и CD пересекаются в точке F. AF равно 8, FB равно 6. CD равно 16. Найти CF и FD.
25 задача

Answer 1

Пусть CF = x, тогда FD = 16 - x.

Воспользовавшись свойством пересекающихся хорд (CF·FD = АF·FB), имеем уравнение

x(16 - x) = 8·6

16x - x² = 8·6

x² - 16x + 48 = 0

x₁ = 4; x₂ = 12

Поскольку (на рисунке) CF < FD, то если CF = 4, имеем FD = 16 - 4 = 12.

Ответ: 4; 12.