Question

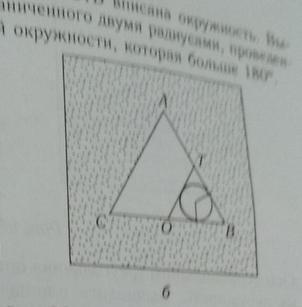
Решете задачу , геометрия 9 класс.На рисунке 86, б изображен равносторонний треугольник АВС, длина стороны которого равна 4 см. Точки О и Т — середины сторон BC и АВ соответственно. В треугольник ОТВ вписана окружность. Вычислите площадь сектора, ограниченного двумя радиусами, проведенными в точки касания, и дугой окружности, которая больше 180°.

Answer 1

Площадь сектора . Есть формула: S = πR²/360°  *  α.

У нашего сектора α = 240° . Осталось найти радиус вписанной окружности.

ΔОТВ - равносторонний со стороной 2 см. в нём высота = √3. R = √3/3

S = π*3/9 : 360° * 240° =2π/9(см²)