Question

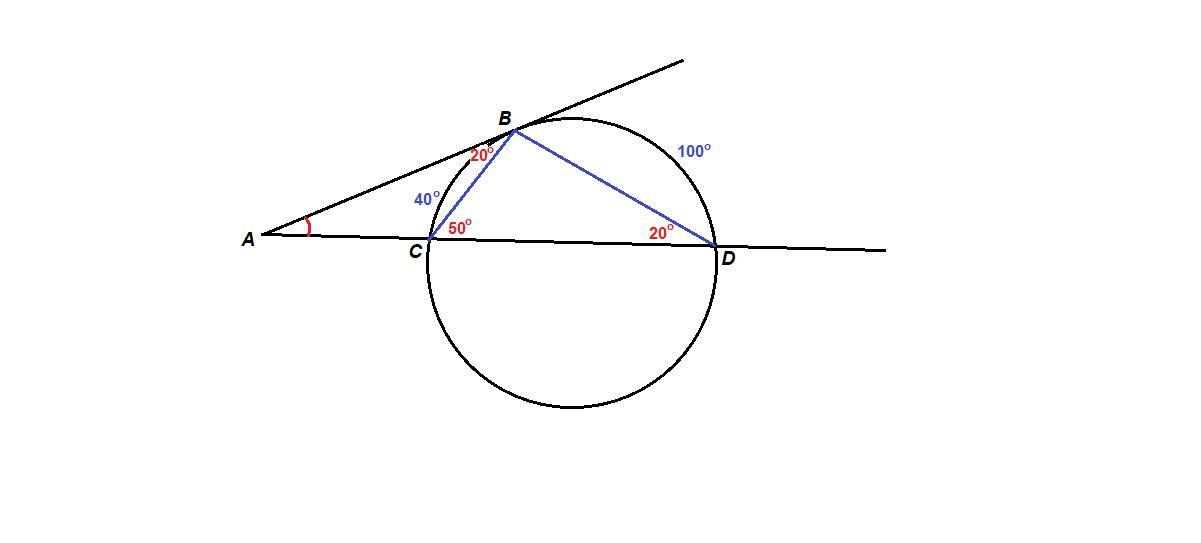
Из точки А ,взятой вне окружности,проведены касательная АВ (В- точка касания) и секущая АД (С и Д точки пересечения с окружностью,С пренадлежит АД) найдите угол ДАВ,если дуга СВ=40°,дуга ДВ=100°

Answer 1

Ответ:  ∠DAB = 30°

Объяснение:

Вписанный угол равен половине дуги, на которую он опирается, значит

∠BCD = 1/2 ∪DB = 1/2 · 100° = 50°

∠BDC = 1/2 ∪CB = 1/2 · 40° = 20°

Угол между касательной и хордой равен половине дуги, заключенной внутри этого угла, значит

∠АВС = 1/2 ∪СВ = 1/2 · 40° = 20°

∠BCD - внешний для треугольника АВС. По свойству внешнего угла

∠BCD = ∠ABC + ∠BAC

∠BAC = ∠BCD - ∠ABC = 50° - 20° = 30°

∠DAB = 30°

_________________________________

Стоит запомнить, что угол между секущими, проведенными из одной точки (или между секущей и касательной, как в данном случае), равен полуразности дуг, заключенных между ними.

∠DAB = 1/2 (∪DB - ∪CB) = 1/2 (100° - 40°) = 1/2 · 60° = 30°