Помогите решить
2/x-1 - 1/x+1 больше 3
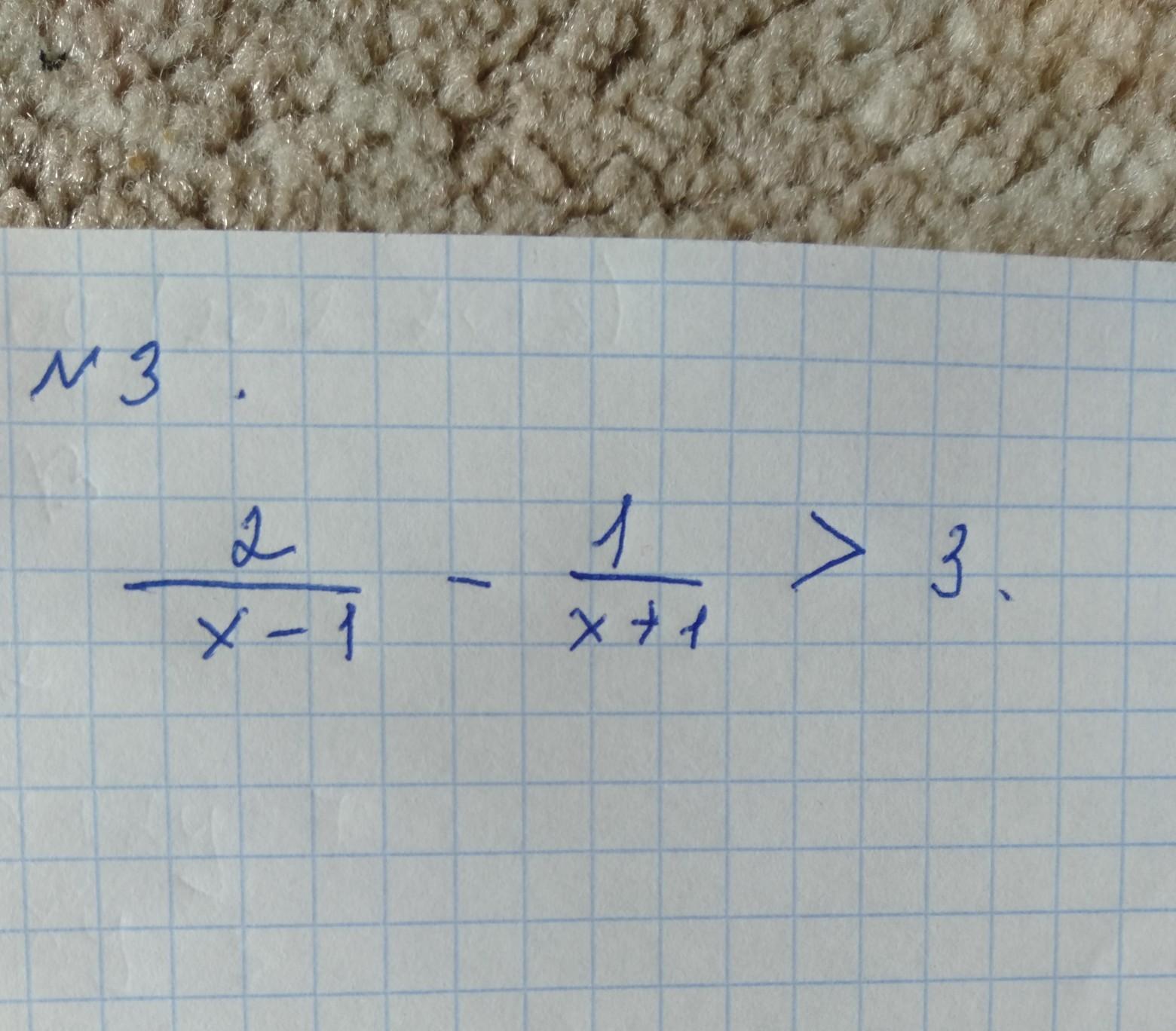
Ответы
Для начала найдём ОДЗ(в нашем случае, знаменатель никогда не равен 0)
Тогда:
х-1≠0;х≠1
х+1≠0;х≠-1
Если эти я числа подставить в знаменатель, тогда там будет 0, а на него делить нельзя.
И так, ОДЗ нашли, теперь давай сведём к общему знаменателю(Нужно знаменатель одной дроби, умножить на числитель и знаменатель другой дроби, и так со всеми)
Значит умножаем первую дробь на х+1 а вторую на х-1
Теперь когда знаменатели равны, можем складывать дробь в 1 целый и заодно тройку влево забросим
Теперь опять ищем общий знаменатель
Видим что (х-1)(х+1) это формула сокращённого умножения в виде а²-b²=(a-b)(a+b)
Собираем всё в одну дробь
Дробь равна нулю тогда, когда числитель равен нулю, решим его
-3х²+х+6=0
D=1-4×(-3)×6=√73
x(1,2)=
Теперь если решить методом интервалов ответ будет
(1-√73/6;-1) объединение (1+√73/6;1)
P.S. плохой ответ, но это правильно =)