Предмет: Математика,
автор: TuRuaz0311
Найти пределы функции
Приложения:
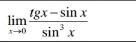
Ответы
Автор ответа:
0
Ответ:
..........................
Пошаговое объяснение:
Приложения:
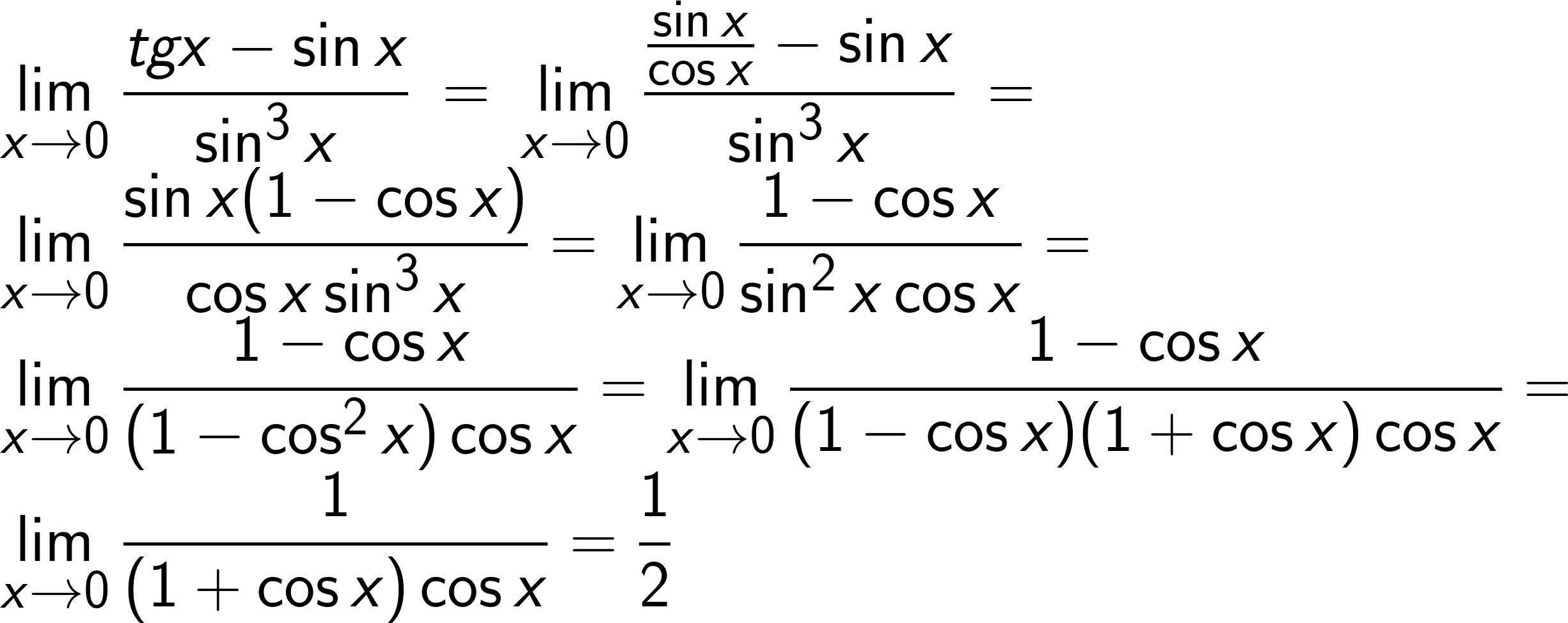
Автор ответа:
0
Ответ:
1/2
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: lilyapotter01
Предмет: Математика,
автор: Chiza0
Предмет: Физика,
автор: Almir77
Предмет: История,
автор: kristinasagradyan
Предмет: История,
автор: grinukjulya