Question

Вычислите площадь фигуры ограниченной линиями y=1+e^x; x+y=2; x=2

Answer 1

Ответ:

1+e^2

Пошаговое объяснение:

1) Построим графики, чтобы понять, какие площади надо будет складывать и вычитать:

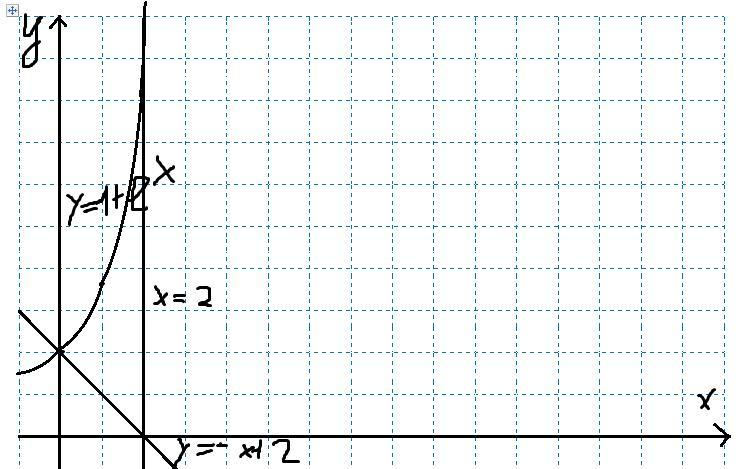
  a) y=1+e^x - показательная функция, проходит через точку (0;2);

  б) y = -x + 2 -линейная функция с угловым коэффициентом -1, проходит через точки (0;2) и (2;0)

  в) x = 2, прямая, параллельная оси ординат (y) проходит через (2;0)

Графики изображены на прикрепленной картинке

2) Заметим, что искомая площадь равна площади под графиком y=1+e^x в промежутке от 0 до 2 минус площадь под графиком y = -x + 2

3) Найдем площадь под графиком y=1+e^x, для этого возьмем определенный интеграл:

$\int\limits^2_0 {1+e^x} \, dx = |^{2}_{0} (x+e^x) = 2+e^2 - 0+e^0=3+e^2$

4) Найдем площадь под графиком y = -x + 2; S = 1/2ab = 1/2*2*2=2

5) вычтем:  S= 3+e^2-2=1+e^2