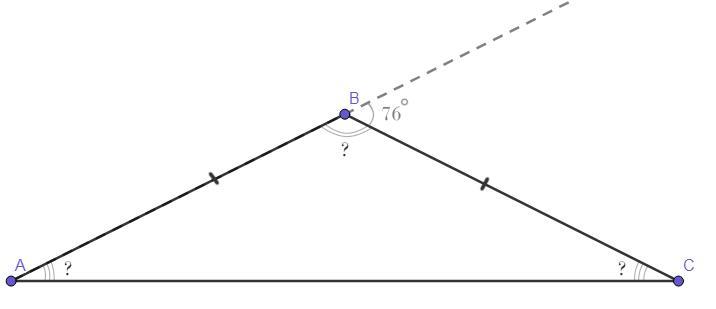
Внешний угол равнобедренного треугольника равен 76 градусов. найдите углы треугольника
Ответы
Чертёж смотрите во вложении.
Дано:
ΔАВС - равнобедренный (АС - основание, АВ = ВС).
Внешний ∠В = 76°.
Найти:
∠АВС = ?
∠ВАС = ?
∠ВСА = ?
Решение:
1) ∠АВС и внешний ∠В - смежные. Сумма смежных углов равна 180°.
Следовательно -
∠АВС+внешний ∠В = 180°
∠АВС = 180°-внешний ∠В
∠АВС = 180°-76°
∠АВС = 104°.
∠ВАС = ∠ВСА - так как это углы у основания равнобедренного треугольника.
По теореме о сумме углов треугольника -
∠ВАС = ∠ВСА = 0,5*(180°-∠АВС)
∠ВАС = ∠ВСА = 0,5*(180°-104°)
∠ВАС = ∠ВСА = 38°.
2) Но давайте рассмотрим второй случай. Допустим, что внешний ∠А или ∠С = 76°.
Угол в 76° - это острый угол. Следовательно, смежные с ними углы будут тупыми. То есть, ∠ВАС и ∠ВСА будут тупыми. А в треугольнике не могут быть два тупых угла (следствие из теоремы о сумме углов треугольника). Поэтому, во 2 случае задача не имеет решений.
Ответ: 104°, 38°, 38°.