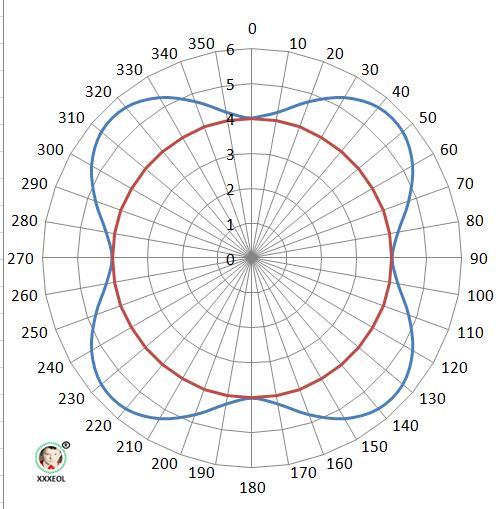
В полярной системе координат построить плоскую фигуру, ограниченную линиями. Найти площадь фигуры вне окружности, произвести все расчеты и написать ответ.
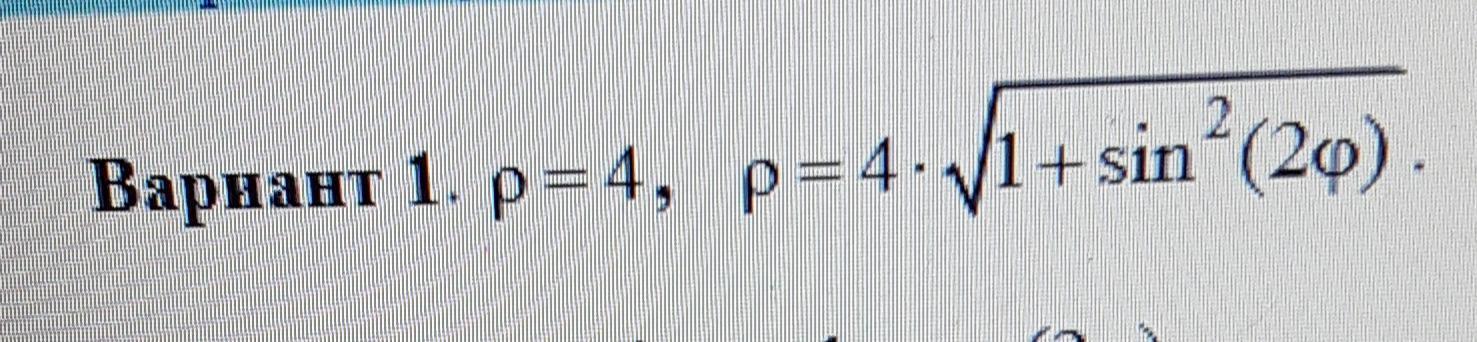
Ответы
ДАНО: - функция, r = 4 - окружность,
НАЙТИ: Площадь фигуры вне окружности.²
Пошаговое объяснение - решение силой Разума.
Мысль 1. Задача в полярных координатах. Построение графика без использования дополнительных средств весьма затратно.
Рисунок с графиком функции при расчёте через 10° в приложении.
Мысль 2. Площадь фигуры - разность площадей функции и окружности с r= 4.
Мысль 3. Площадь окружности по формуле: S1 = π*r² = 16π - (запоминаем - потом надо вычесть).
Мысль 4. Площадь ограниченная функцией по формуле:
Пределы интегрирования от а = 0, до b = 2π - запоминаем.
Мысль 5. Вычисляем значение R(α)²
R(α)² = 16*(1 + sin²2α).
Коэффициент 16 выносим из под интеграла и приступаем собственно к интегрированию.
Делаем подстановку - sin²x = (1-cos2x)/2 и получаем новый интеграл.
В результате получили функцию площади .
Вычисляем на границах интегрирования.
S2(2π) = 8*3π = 24π и S2(0) = 0 и
S2 - 24*π - площадь функции.
И переходим к ответу - вычитаем площадь центрального круга.
S = S2 - S1 = 24*π - 16*π = 8π (ед.²) - площадь фигуры - ответ.