Предмет: Алгебра,
автор: xxxuz
Нужно найти лимит. ............
Приложения:
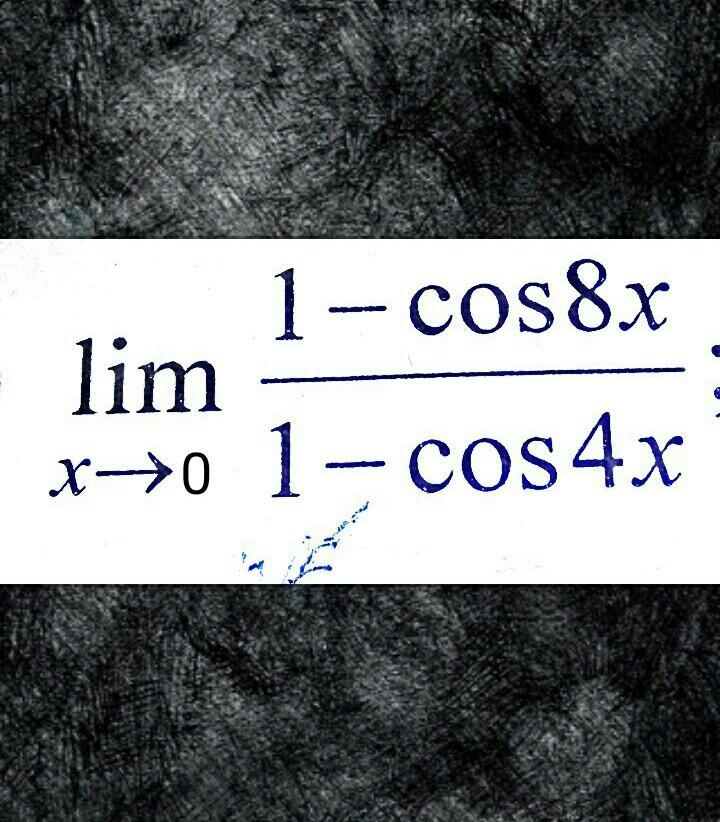
Ответы
Автор ответа:
2
Ответ: 4
Объяснение:
Автор ответа:
0
Ответ: lim(x→0) (1-cos(8x))/(1-cos(4x))=4.
Объяснение:
lim(x→0) (1-cos(8x))/(1-cos(4x))
(1-cos(8x))/(1-cos(4x))=
=(sin²(4x)+cos²(4x)-cos²(4x)+sin²(4x))/(sin²(2x)+cos²(2x)-cos²(2x)+sin²(2x))=
=2*sin²(4x)/(2*sin²(2x)=(2*sin(2x)*cos(2x))²/sin²(2x)=
=4*sin²(2x)*cos²(2x)/sin²(2x)=4*cos²(2x). ⇒
lim(x→0) (4*cos²(2x))=4*1²=4*1=4.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: dashazubareva25
Предмет: Физика,
автор: wwweuh
Предмет: Информатика,
автор: yroslavvivsynikvital
Предмет: Математика,
автор: катякулик12345
Предмет: Математика,
автор: кмка