Предмет: Алгебра,
автор: timur6726
Пожалуйста,срочноооо
Дам 30 балловвв
Найдите корни уровнения
Приложения:
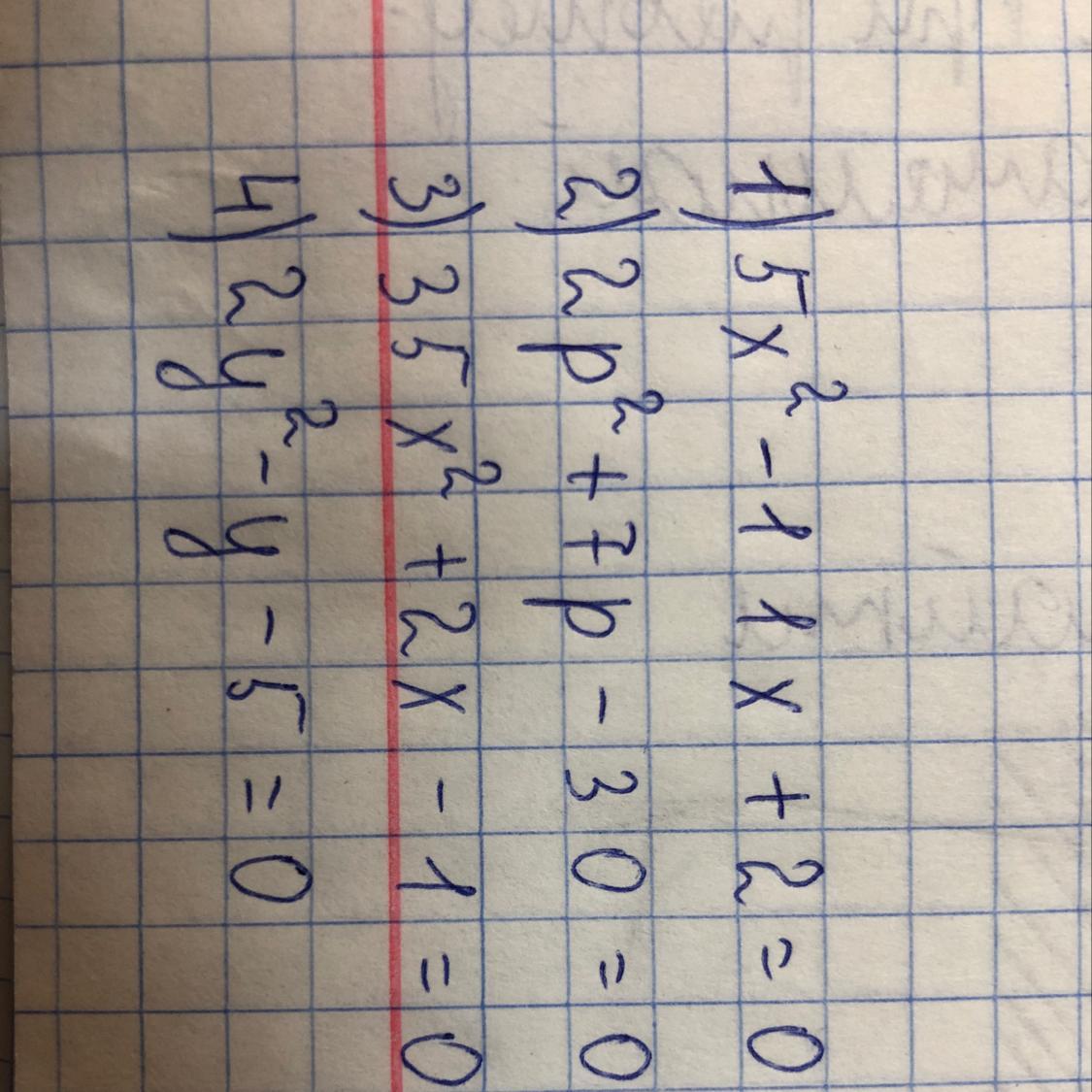
Vasily1975:
Здесь "урОвнений" целых 4. Какое именно урАвнение нужно решить?
Все
Тогда так надо и писать.
Ответы
Автор ответа:
3
В задании приведены квадратные уравнения.
Их можно решать через дискриминант.
Тогда корни уравнения.
Каждую букву я взял в скобки, если получиться уравнение вида
x^2-4x-9, то b= -4; c= -9
И так преступаем к решению.
Решить можно не только через дискриминант, но и путём выделения полного квадрата.
Да знаю, но как я уже понял для нахождения корней удобней использовать дискриминант, это в принципе одно и то же, только с выделением можно допустить больше ошибок.
Можно решать и разложение на множители и иногда через теорему Виета.
Можно решать и разложение на множители и иногда через теорему Виета.
Можно и так. Насчёт же большего ошибок при решении выделением полного квадрата - вопрос спорный.
2y^2-y-5=0
2(y^2-2*1y/4+1/16-1/16)-5=0
2(y-1/4)^2-5-1/8=0
(y-1/4)^2=41/4
При складывании вычитании дроби можно допустить ошибку
Проще было решить через дискриминант.
2(y^2-2*1y/4+1/16-1/16)-5=0
2(y-1/4)^2-5-1/8=0
(y-1/4)^2=41/4
При складывании вычитании дроби можно допустить ошибку
Проще было решить через дискриминант.
Вам, может быть, и проще, мне - совершенно одинаково. Поэтому остаюсь при своём мнении и считаю дискуссию завершённой.
Похожие вопросы
Предмет: Алгебра,
автор: Dandellion
Предмет: Английский язык,
автор: zibekloskarova
Предмет: Алгебра,
автор: malyginnikita48
Предмет: Математика,
автор: CharryRad2000