Предмет: Физика,
автор: Fromoon
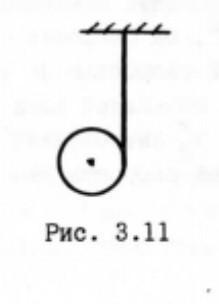
На сплошной цилиндр массы M намотана тонкая нить, свободный конец которой прикреплён к потолку. Найти ускорение, с которым цилиндр опускается под действием силы тяжести, и силы натяжения нити.
Приложения:
Ответы
Автор ответа:
6
Ответ:
Объяснение:
мгновенная ось вращения у цилиндра находится справа в точке касания с нитью.
2 закон ньютона для вращательного движения
M=J*e
M=mg*R - момент силы тяжести относительно мгновенной оси
J=J0+mR^2 - момент инерции относительно мгновенной оси по теореме Штейнера
J0=1/2*mR^2 - осевой момент инерции сплошного однородного цилиндра
=>
J = 1/2*mR^2 + mR^2 = 3/2*mR^2
e=M/J = mg*R : 3/2*mR^2 = 2/3*g/R - угловое ускорение вращательного движения
a=e*R=2/3*g - искомое ускорение с которым опускается цилиндр.
по 2 закону ньютона
mg-T=ma
T=m(g-a)=m*g/3 - искомая сила натяжения
**********************************
в решении приняты обозначения M - момент сил, m - масса
мне так привычнее. хотите - переобозначайте.
IUV:
можно было решать на основании закона сохранения энергии. но тоже пришлось бы использовать понятие момента инерции
Похожие вопросы
Предмет: Алгебра,
автор: kirillmisenko882
Предмет: Алгебра,
автор: Timtimjfjc
Предмет: Математика,
автор: robot228535
Предмет: Математика,
автор: Maziaka001
Предмет: Математика,
автор: Аноним