Предмет: Алгебра, автор: WhatYouNeed

$\sin^2{2x}+|\sin{2x}|=4\cos^2{x}$
Решите уравнение с полным оформлением.

Nullpo201: Я, конечно, задачу не решу, но как записывать задачи в таком виде?

WhatYouNeed: Ну можно раскрыть модуль по определению и решать тригонометрическое равенство, преобразовывая выражения и раскладывать на произведение простейших тригонометрических выражений: (cosx+1)(sin^2x-1)=0
Или построить две функции (с объяснениями) и найти их пересечение.

WhatYouNeed: Или выразить всё выражение через одну функцию и построить её.
Или выразить всё через функцию, где есть переменные только вида cosx, без sin x tan x cot x ну или sin x, а затем построить в декартовых координатах и найти решение на тригонометрическом круге: cos x -sin^2x=0 => cos x = sin^2x => x=y^2 и x^2+y^2=1 найти пересечение.

Nullpo201: Я не про это, как красиво записать задачу/решение, а то с использованием клавиатуры это выходит проблематично

WhatYouNeed: А ну тут есть редактор, вот видите я записал степень в верхнем индексе sin и cos тоже как отдельное выражение, а не просто буквами: \sin{x} \cos{x} \tan{x} если пользоваться этим редактором больше месяце то уже привыкаешь ко всякому, я даже придумал как квадратные скобки ставить, а не фигурные. Ну то есть написали что-то дальше если надо, то поясняете, а так всё тоже самое, что и в тетради. Хотя можно решить в тетради и прислать фотографию

Ответы

Автор ответа: dimaogol2000

Ответ:

Объяснение:

////////////////////////////////

Приложения:

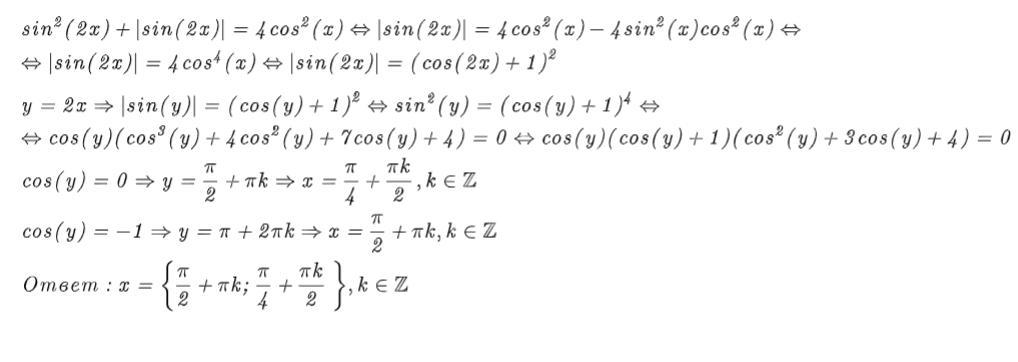
WhatYouNeed: После замены переменной 3 переход слишком быстрый можно было и по подробнее, а так же можно было сказать, что третья скобка все положительная, то есть не равняется нулю. А в остальном всё супер, спасибо.

dimaogol2000: Да.Можно было расписать по формуле a^2-b^2 и преобразовывать ,но я увидел ,что вы уже предлагали способы решения и подумал что не зачем )))

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Английский язык, автор: djalgasovarman064