Предмет: Алгебра,
автор: Slayertj
Решить предел при помощи алгебраических преобразований (не правило Лопиталя)
Приложения:
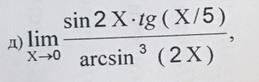
Slayertj:
да
Ответы
Автор ответа:
2
Ответ: ∞.
Объяснение:
Воспользуемся эквивалентностью функций:
Похожие вопросы
Предмет: Биология,
автор: dbaranovskii2010
Предмет: Геометрия,
автор: kseniya8573
Предмет: Биология,
автор: zohbaxtiyarovzero678
Предмет: Математика,
автор: Dari0509
Предмет: Алгебра,
автор: spiridonowaksena