Предмет: Алгебра, автор: WhatYouNeed

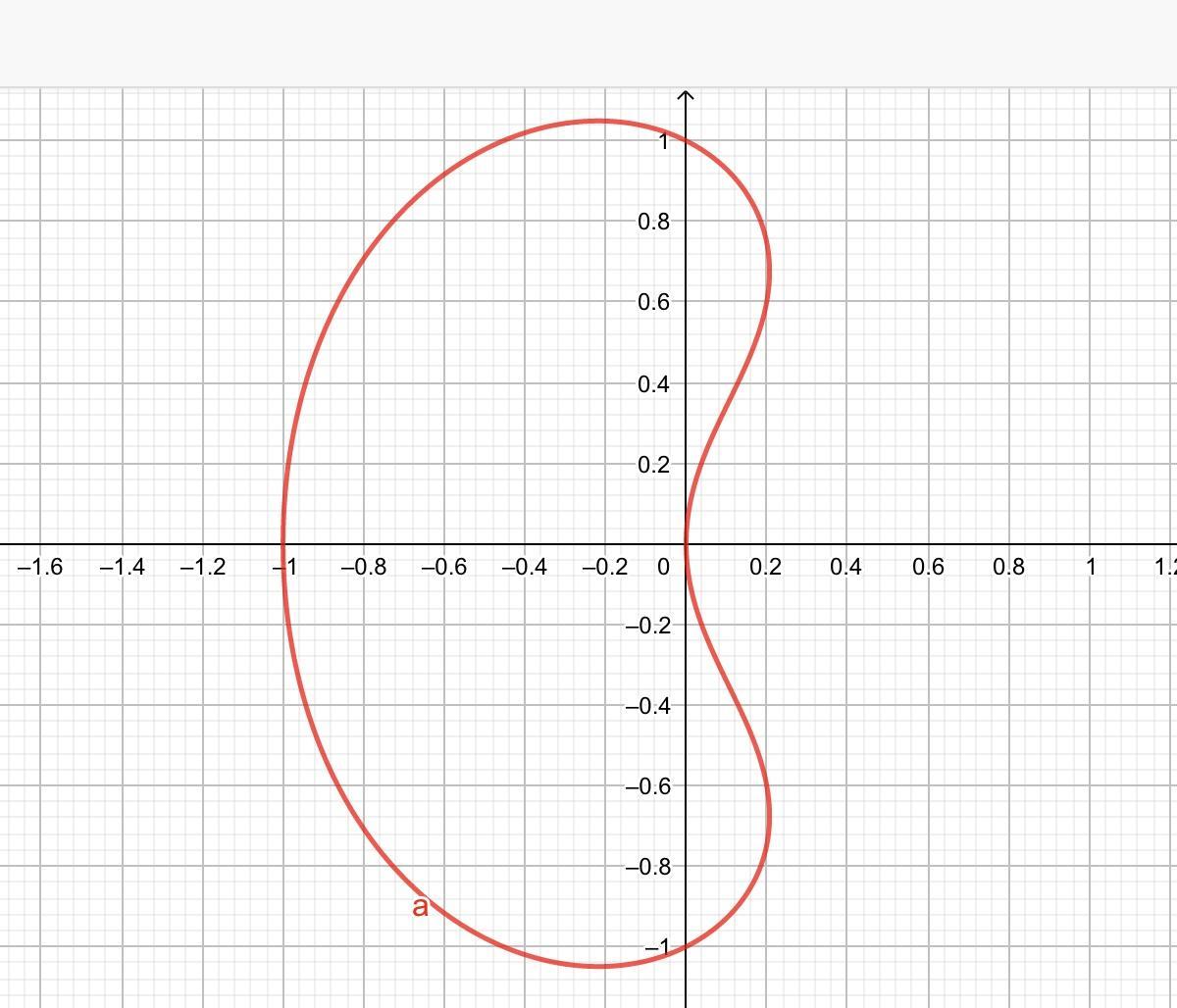
Постройте график уравнения, с пояснениями. $(x^2+y^2)^2=y^2-x$ Как строить графике уравнений если нельзя выразить через функцию и построить график функции?

antonovm: А почему нельзя выразить y через х , очень даже можно и полярные координаты сгодятся , щас решение ( исследование ) напишу

Ответы

Автор ответа: antonovm

Ответ:

Объяснение:

В решении переменную х считаю параметром и нахожу все значения x , при которых полученное биквадратное уравнение относительно переменной y имеет хотя бы одно решение , далее просто решаю биквадратное уравнение при найденных х

Приложения:

WhatYouNeed: При последнем подсчёте точки вы не правильно посчитали дискриминант 16t^2-8t-7=0
8t^2-4t-3.5=0
D=16+16*7=8*16=128 =>
4+sqrt(128)
Спасибо за помощь, я конечно ожидал схематического построение графика, но найти промежуток существования уравнения по оси Ох вполне не плохо. Я так и думал, что график этого уравнения без подстановки значения по одной из переменных, построить достаточно затруднительно.

antonovm: сейчас исправлю ( дискриминант ) , полярные координаты также сойдут , там можно косинус ( угол) через расстояние выразить

antonovm: а вообще из нее хорошая задача с параметром выйдет ( 2 решения , 3 и тд ) , пожалуй своим ученикам предложу

antonovm: Вы можете получить формулу y через х , только это не будет функцией + - , а еще забыл написать , что y входит в уравнение в квадрате , а значит фигура симметрична относительно оси ОХ

WhatYouNeed: А можете описать каким образом дано уравнение свести к полярные координатам r=f (cos a) ? Я только имеют представление как строить простейшие графики в полярных координатах, а как к ним сводить я не знаю

antonovm: x =r cosa ; y = r sina x^2 +y^2 = r^2 ; ( x^2 +y^2) ^2 = r^4 ; подставляете все это в уравнение , сокращаете на r и получаете формулу , переходите к косинусу ( sin^2x = 1 -cos^2x) и получите квадратное уравнение относительно косинуса , далее задаете угол , по углу косинус , а по нему расстояние

WhatYouNeed: Спасибо.

antonovm: не то написал , здесь косинус выражается через расстояние , а если наоборот , то кубическое уравнение получится

antonovm: все таки мой способ лучший , почти школьный

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Информатика, автор: e2e4stm

5. У исполнителя Альфа две команды, которым присвоены номера: 1. прибавъ 1 2. умножь на b ( неизвестное натуральное число; b =>2) Выполняя первую из них, Альфа увеличивает число на экране на 1, а выполняя вторую, умножает это число на b. Программа для исполнителя Альфа — это последовательность номеров команд Известно, что программа 11221 переводит число 2 в число 65. Определите значение b.

6 лет назад

Предмет: Окружающий мир, автор: maryanyanraya

Какую продукцию выпускал Путиловский завод в 19 веке?
Кратко. СРОЧНОООО!!!

6 лет назад